Lecture
Blind Signature ( Blind Signature ) is a type of EDS, a feature of which is that the signer cannot know the exact contents of the document being signed. The concept of a blind signature was invented by David Chaum ( Eng. ) [1] in 1982, he also proposed the first implementation through the RSA algorithm. The security of the blind signature scheme was based on the difficulty of factoring large compound numbers. Since then, a large number of other schemes have been proposed [2] [3].
The main idea of blind signatures is as follows:
Upon completion of this protocol, Party B does not know anything about the message t, nor about the signature of this message.
This scheme can be compared with the envelope in which the document and the copying sheet are placed. If you sign an envelope, the signature will be imprinted on the document, and when the envelope is opened, the document will already be signed.
The purpose of a blind signature is to prevent the signer B from reading the message of party A, which he signs, and with the corresponding signature under this message. Therefore, in the future, the signed message cannot be associated with party A.
The secure blind signature scheme should satisfy 3 properties, namely:
1) Zero disclosure . This property helps the user to get a signature on this message without disclosing the message to the signer.
2) non-traceability . The signer cannot track a signature-message pair after the user has published a signature on his message.
3) The simplicity . Only the signer can generate a valid signature. This property is the most important and must be satisfied for all signature schemes.
Due to the properties of zero disclosure and non-traceability, the blind signature scheme can be widely used in applications that require confidentiality, for example, in electronic voting systems [4] [5] [6] [7].
Given the situation: Bob - notary. Alice needs him to sign the document, having no idea about its content. Bob only assures that the document is notarized at the indicated time. Then they act according to the following algorithm:
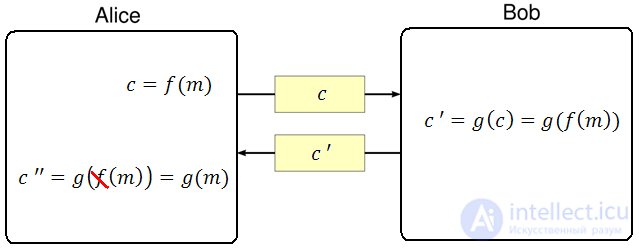
In this scheme, Alice wants Bob to blindly sign the message {\ displaystyle m}  . For this:
. For this:
 function {\ displaystyle f}
function {\ displaystyle f}  receiving the encrypted message {\ displaystyle c = f (m)}
receiving the encrypted message {\ displaystyle c = f (m)}  .
.  function {\ displaystyle g}
function {\ displaystyle g}  , getting {\ displaystyle c ^ {'} = g (c) = g (f (m))}
, getting {\ displaystyle c ^ {'} = g (c) = g (f (m))}  .
.  back to Alice.
back to Alice.  and removes its encryption by getting: {\ displaystyle c ^ {''} = g (f (m)) * f ^ {- 1} = g (m)}
and removes its encryption by getting: {\ displaystyle c ^ {''} = g (f (m)) * f ^ {- 1} = g (m)}  .
. This protocol works only if the signature and encryption functions are commutative.
RSA protocol
The first implementation of blind signatures was carried out by Chaum using the RSA cryptosystem:
Suppose that initially Bob has a public key {\ displaystyle (p, e)}  where {\ displaystyle p}
where {\ displaystyle p}  is a module, and {\ displaystyle e}
is a module, and {\ displaystyle e}  - public key exponent.
- public key exponent.
 mutually simple with {\ displaystyle p}
mutually simple with {\ displaystyle p}  , and computes {\ displaystyle m ^ {'} \ equiv mr ^ {e} {\ bmod {p}}}
, and computes {\ displaystyle m ^ {'} \ equiv mr ^ {e} {\ bmod {p}}}  .
.  through the open channel to Bob.
through the open channel to Bob.  using your private key {\ displaystyle (p, d)}
using your private key {\ displaystyle (p, d)}  .
.  back to Alice.
back to Alice.  as follows: {\ displaystyle s \ equiv s ^ {'} * r ^ {- 1} {\ bmod {p}} \ equiv m ^ {d} {\ bmod {p}}}
as follows: {\ displaystyle s \ equiv s ^ {'} * r ^ {- 1} {\ bmod {p}} \ equiv m ^ {d} {\ bmod {p}}}  .
. Chaum invented a whole family of more complex blind signature algorithms under the general name unexpected blind signatures . Their schemes are even more complicated, but they provide more opportunities [1].
Blind signature based on EDS Schnorr
Let Alice want to sign the message {\ displaystyle m}  in Bob so that, firstly, Bob could not get acquainted with the message during the signature, secondly, so that Bob could not subsequently receive the message {\ displaystyle m}
in Bob so that, firstly, Bob could not get acquainted with the message during the signature, secondly, so that Bob could not subsequently receive the message {\ displaystyle m}  and the corresponding signature to identify the user who initiated the blind signature protocol for this particular message (Alice). This protocol is implemented as follows:
and the corresponding signature to identify the user who initiated the blind signature protocol for this particular message (Alice). This protocol is implemented as follows:
 .
.  (w and t are random numbers not exceeding {\ displaystyle y}
(w and t are random numbers not exceeding {\ displaystyle y}  ), {\ displaystyle E ^ {'} = H (m || R ^ {'})}
), {\ displaystyle E ^ {'} = H (m || R ^ {'})}  and {\ displaystyle E = E ^ {'} + t \ mod y}
and {\ displaystyle E = E ^ {'} + t \ mod y}  and then sends Bob the value {\ displaystyle E}
and then sends Bob the value {\ displaystyle E}  .
.  such that {\ displaystyle R = a ^ {S} y ^ {E} \ mod p}
such that {\ displaystyle R = a ^ {S} y ^ {E} \ mod p}  and sends {\ displaystyle S}
and sends {\ displaystyle S}  Alice
Alice  where {\ displaystyle E ^ {'} = E ^ {- t} \ mod y}
where {\ displaystyle E ^ {'} = E ^ {- t} \ mod y}  and {\ displaystyle S ^ {'} = Sw \ mod y}
and {\ displaystyle S ^ {'} = Sw \ mod y}  which is genuine with respect to the message {\ displaystyle m}
which is genuine with respect to the message {\ displaystyle m}  [eight].
[eight]. Evidence
The authenticity of the signature is proved as follows. From {\ displaystyle R = a ^ {S} y ^ {E} \ mod p}  should {\ displaystyle Ra ^ {- w} y ^ {- t} = a ^ {Sw} y ^ {Et} modp}
should {\ displaystyle Ra ^ {- w} y ^ {- t} = a ^ {Sw} y ^ {Et} modp}  and {\ displaystyle R ^ {'} = a ^ {S ^ {'}} y ^ {E ^ {'}} \ mod p}
and {\ displaystyle R ^ {'} = a ^ {S ^ {'}} y ^ {E ^ {'}} \ mod p}  . In this case, the problem of anonymity is solved, since any triple {\ displaystyle (R, S, E)}
. In this case, the problem of anonymity is solved, since any triple {\ displaystyle (R, S, E)}  from the set of such triples that were formed by Bob, can be matched with the signature {\ displaystyle (E ^ {'}, S ^ {'})}
from the set of such triples that were formed by Bob, can be matched with the signature {\ displaystyle (E ^ {'}, S ^ {'})}  to this document {\ displaystyle m}
to this document {\ displaystyle m}  . Indeed, we have: {\ displaystyle R = a ^ {S} y ^ {E} \ mod p}
. Indeed, we have: {\ displaystyle R = a ^ {S} y ^ {E} \ mod p}  and {\ displaystyle R ^ {'} = a ^ {S ^ {'}} y ^ {E ^ {'}} \ mod p}
and {\ displaystyle R ^ {'} = a ^ {S ^ {'}} y ^ {E ^ {'}} \ mod p}  {\ displaystyle \ Rightarrow}
{\ displaystyle \ Rightarrow}  {\ displaystyle R ^ {'} / R \ equiv a ^ {S ^ {'} - S} y ^ {E ^ {'} - E} \ mod p \ equiv a ^ {- w} y ^ {- t } \ mod p}
{\ displaystyle R ^ {'} / R \ equiv a ^ {S ^ {'} - S} y ^ {E ^ {'} - E} \ mod p \ equiv a ^ {- w} y ^ {- t } \ mod p}  i.e. with an equiprobable random selection of the terms {\ displaystyle w}
i.e. with an equiprobable random selection of the terms {\ displaystyle w}  and {\ displaystyle t}
and {\ displaystyle t}  signature {\ displaystyle (E ^ {'}, S ^ {'})}
signature {\ displaystyle (E ^ {'}, S ^ {'})}  with equal probability, it was generated from any triplet included in the set of triples formed by the signer. Note also that Bob does not even have the opportunity to prove that at the time of the signature of this document {\ displaystyle m}
with equal probability, it was generated from any triplet included in the set of triples formed by the signer. Note also that Bob does not even have the opportunity to prove that at the time of the signature of this document {\ displaystyle m}  he was not acquainted with him.
he was not acquainted with him.
Blind signature based on GOST R 34.10-94
Options:
p is a prime number, 510 ≤ | p | ≤ 512 (or 1022 ≤ | p | ≤ 1024), where | p | - the bit width of the binary representation of the number p.
q is a large prime divisor of p-1, 255 ≤ | q | ≤ 256 (or 511 ≤ | q | ≤ 512)
α ≠ 1, α < p , {\ displaystyle \ alpha ^ {q}}  mod p = 1.
mod p = 1.
Calculation:
 mod p ) mod q is the first part of the signature;
mod p ) mod q is the first part of the signature; Check:
 mod p ) mod q , where y is the public key;
mod p ) mod q , where y is the public key; Blind signature based on STB 1176.2-99 standard
The Belarus standard provides the following protocol for generating a blind signature to the document M :
 . These actions are performed by the signer. Next, it passes the number R to the user;
. These actions are performed by the signer. Next, it passes the number R to the user;  , {\ displaystyle E '= F_ {H} (R' || M)}
, {\ displaystyle E '= F_ {H} (R' || M)}  and E = E ' - τ mod q ; E - the first element of the signature - sent to the signer;
and E = E ' - τ mod q ; E - the first element of the signature - sent to the signer; In this description, the following parameters are used: q - the module used for calculations is simple; a is the generating element; x - private key; y is the public key [9].
Let {\ displaystyle {\ overline {y_ {1}, y_ {s}}}}  - public keys owned by s users. Suppose there is a message M that m of them want to sign. In this case, all the signatures can be combined into one, the length of which is equal to the length of the signature of one user and does not depend on m . This is implemented according to the rules of the following protocol:
- public keys owned by s users. Suppose there is a message M that m of them want to sign. In this case, all the signatures can be combined into one, the length of which is equal to the length of the signature of one user and does not depend on m . This is implemented according to the rules of the following protocol:
 < p , where j = {\ displaystyle {\ overline {1, m}}}
< p , where j = {\ displaystyle {\ overline {1, m}}}  , p is a large prime number. Then each of the m users calculates {\ displaystyle R _ {\ alpha _ {j}} = (t _ {\ alpha _ {j}}) ^ {k}}
, p is a large prime number. Then each of the m users calculates {\ displaystyle R _ {\ alpha _ {j}} = (t _ {\ alpha _ {j}}) ^ {k}}  mod p ( k is a large simple degree) and sends this number to all other users from this group.
mod p ( k is a large simple degree) and sends this number to all other users from this group.  mod p . Next, e = f (R, M) = RH mod q is calculated, where q is a large prime number other than p , H = Hash (M) is a hash function. The number e will be the first element of the collective signature.
mod p . Next, e = f (R, M) = RH mod q is calculated, where q is a large prime number other than p , H = Hash (M) is a hash function. The number e will be the first element of the collective signature.  mod p - user share. Each user calculates and shares this share.
mod p - user share. Each user calculates and shares this share.  mod p . This is the second element of the collective signature.
mod p . This is the second element of the collective signature. Collective blind signature verification
{\ displaystyle y = \ prod _ {j = 1} ^ {m} y _ {\ alpha _ {j}}}  mod p is a shared public key. Based on this, a collective blind signature is verified using the following algorithm:
mod p is a shared public key. Based on this, a collective blind signature is verified using the following algorithm:
 mod p .
mod p . The most widely used protocol for blind signatures found in the field of digital money. For example, in order for the depositor not to deceive the bank, such a protocol can be used: the depositor writes the same denomination of bills on a hundred documents with different numbers and deposits it in encrypted form with the bank. The bank chooses at random and demands to open 99 (or n-1) envelopes, makes sure that $ 10 is written everywhere, not $ 1000, then signs the remaining envelope blindly, without seeing the bill number.
A simpler option may be provided: for each denomination of a banknote, a bank has its own pair of public keys. Then, only the bill number is sent under the signature, and the need to verify the nominal value before the signature disappears [1].
Blind signatures are used for secret voting. In the protocol of Fujioka, Okamoto and Ohta, the voter prepares a ballot paper with his choice, which he made, encrypts it with a secret key, and disguises it. Then the voter signs the ballot and sends it to the validator. The validator verifies that the signature belongs to a registered voter who has not yet voted.
If the ballot is valid, the validator signs the ballot and returns it to the voter. The voter removes the disguise, thus revealing the encrypted ballot signed by the validator. Next, the voter sends the resulting signed, encrypted ballot to the counter, which verifies the signature on the encrypted ballot.
If the ballot is valid, the counter places it on the list that will be issued after the entire vote. After the list is issued, voters verify that their ballots are on the list and send the decryption keys necessary for opening their ballots to the counter. The counter uses these keys to decrypt ballots and adds a voice to the total. After the election, the counter issues decryption keys along with encrypted ballots so that voters can independently verify the choice [10].
The RSA algorithm can be the object of an attack, thanks to which it becomes possible to decrypt a previously signed blind message, passing it off as a message that has yet to be signed. Based on the fact that the signature process is equivalent to deciphering by the signer (using its secret key), an attacker can attach to the signature an already signed blind version of the message {\ displaystyle m}  encrypted with the signer's public key, i.e. enclose message {\ displaystyle m '}
encrypted with the signer's public key, i.e. enclose message {\ displaystyle m '}  .
.
{\ displaystyle {\ begin {aligned} m '' & = m'r ^ {e} {\ pmod {n}} \\ & = (m ^ {e} {\ pmod {n}} \ cdot r ^ { e}) {\ pmod {n}} \\ & = (mr) ^ {e} {\ pmod {n}} \\\ end {aligned}}} 
where {\ displaystyle m '}  - This is an encrypted version of the message. When the message is signed, the plaintext {\ displaystyle m}
- This is an encrypted version of the message. When the message is signed, the plaintext {\ displaystyle m}  easy to extract:
easy to extract:
{\ displaystyle {\ begin {aligned} s' & = m '' ^ {d} {\ pmod {n}} \\ & = ((mr) ^ {e} {\ pmod {n}}) ^ {d } {\ pmod {n}} \\ & = (mr) ^ {ed} {\ pmod {n}} \\ & = m \ cdot r {\ pmod {n}} {\ mbox {, since}} ed \ equiv 1 {\ pmod {\ phi (n)}} \\\ end {aligned}}} 
where {\ displaystyle \ phi (n)}  - This is Euler's function. Now the message is easy to get.
- This is Euler's function. Now the message is easy to get.
{\ displaystyle {\ begin {aligned} m = s' \ cdot r ^ {- 1} {\ pmod {n}} \ end {aligned}}} 
The attack works because in this scheme the signer directly signs the message itself. In contrast, in conventional signature schemes, the signer typically signs, for example, a cryptographic hash function. Therefore, because of this multiplicative property of RSA, one key should never be used simultaneously for encryption and blind signing [8].
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis