Random moments

The random variable magnitude is the numerical characteristic of the distribution of a given random variable.

Definitions

If given a random variable 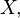defined on a certain probability space, then:

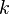• initial moment of random variabl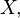e Where 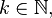called magnitude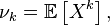

if the expectation is 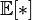on the right side of this equation is defined;

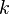• th center moment of a random variable 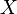called magnitude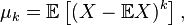

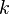• absolutist and 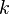m absolute absolute moments of a random variable 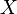is called according to size

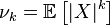and

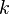• m factorial moment of a random variable 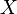called magnitude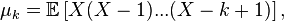

if the expectation on the right side of this equation is defined. ^[one]

Absolute moments can be defined not only for integers 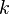but for any positive real if the corresponding integrals converge.

Remarks

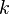• If points are defined th order, then determined and all the moments of lower orders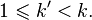
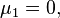
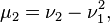
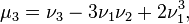
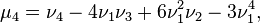• By virtue of the linearity of the expectation, the central moments can be expressed in terms of the initial ones, and vice versa. For example:

etc.

Geometrical meaning of some moments

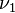• equals the mathematical expectation of a random variable and shows the relative location of the distribution on the number line.
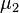• equals the distribution variance 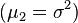and shows the spread of the distribution around the mean.
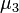• being properly normalized, is a numerical characteristic of the symmetry of the distribution. More precisely, the expression

called the asymmetry coefficient.

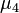• controls how pronounced the vertex of the distribution is in the neighborhood of the middle. Magnitude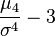

called the coefficient kurtosis kurtosis distribution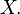

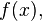Calculation of moments

• Moments can be calculated directly through the definition by integrating the corresponding degrees of the random variable. In particular, for an absolutely continuous distribution with density we have: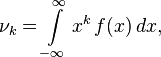

if a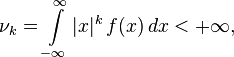

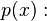
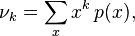
if a

• Also, the moments of a random variable can be calculated through its characteristic function. :

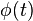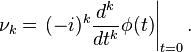
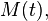• If the distribution is such that for it in some neighborhood of zero the generating function of moments is defined then the moments can be calculated by the following formula: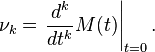

Generalizations

You can also consider non-integer values. 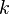. Moment considered as a function of the argument 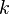is called the Mellin transform.

You can consider the moments of a multidimensional random variable. Then the first moment will be a vector of the same dimension, the second will be a second-rank tensor (see covariance matrix) over a space of the same dimension (although a trace of this matrix can be considered, which gives a scalar generalization of the variance). Etc.