7.4 Numerical Characteristics of the Statistical Distribution

In Chapter 5, we introduced into consideration various numerical characteristics of random variables: expectation, variance, initial and central moments of various orders. These numerical characteristics play a large role in probability theory. Similar numerical characteristics exist for statistical distributions. Each numerical characteristic of a random variable 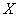corresponds to its statistical analogy. For the basic characteristic of a position — the mathematical expectation of a random variable — this is the arithmetic average of the observed values ​​of a random variable:

, (7.4.1)

Where 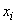- random variable observed 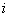m experience 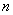- the number of experiences.

This characteristic will be referred to as the statistical average of a random variable.

According to the law of large numbers, with a limited increase in the number of experiments, the statistical average approaches (converges in probability) to the mathematical expectation. With a limited number of experiments, the statistical average is a random variable, which, nevertheless, is associated with the expectation and can give a known idea about it.

Similar statistical analogies exist for all numerical characteristics. Let us further agree on these statistical analogies in the same letters as the corresponding numerical characteristics, but also provide them with the * symbol.

Consider, for example, the variance of a random variable. It is a mathematical expectation of a random variable. :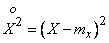

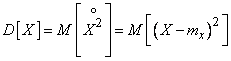. (7.4.2)

If in this expression we replace the expectation with its statistical analogy — the arithmetic average, we get the statistical variance of the random variable :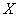

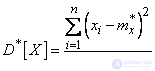, (7.4.3)

Where 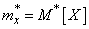- statistical average.

The statistical initial and central moments of any order are determined similarly:

(7.4.4)

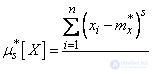(7.4.5)

All these definitions are completely analogous to the definitions of numerical characteristics of a random variable given in Chapter 5, with the difference that the arithmetic average appears everywhere instead of the mathematical expectation. With an increase in the number of observations, obviously, all statistical characteristics will converge in probability to the corresponding mathematical characteristics and with sufficient can be taken approximately equal to them.

It is not difficult to prove that for statistical initial and central moments the same properties are valid, which were introduced in Chapter 5 for mathematical moments. In particular, the statistical first central moment is always zero:

.

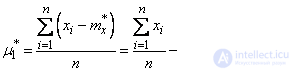The ratios between the central and initial moments also remain:

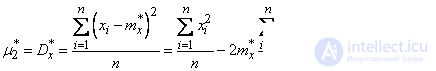(7.4.6)

etc.

With a very large number of experiments, the calculation of characteristics using the formulas (7.4.1) - (7.4.5) becomes excessively cumbersome and you can apply the following technique: use the same bits to which statistical material was classified to build a statistical series or histogram, and take it approximately the value of the random variable in each digit is constant and equal to the mean value, which acts as a “representative” of the digit. Then the statistical numerical characteristics will be expressed by approximate formulas:

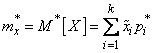, (7.4.7)

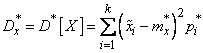, (7.4.8)

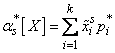, (7.4.9)

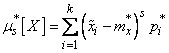, (7.4.10)

Where 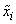- “representative” 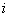th discharge, 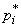- frequency 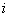th discharge, 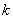- number of digits.

As you can see, formulas (7.4.7) - (7.4.10) are completely analogous to formulas 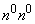5.6 and 5.7, determining the expectation, variance, initial and central moments of a discontinuous random variable 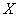, with the only difference that instead of probabilities 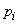there are frequencies in them 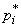instead of mathematical expectation 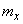- statistical average 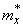, instead of the number of possible values ​​of a random variable - the number of digits.

In most of the manuals on probability theory and mathematical statistics, when considering the issue of statistical analogies, terminology is used to characterize random variables, which is somewhat different from that adopted in this book, namely, the statistical average is referred to as the “sample mean”, the statistical variance is called the “sample variance” and t .d

The origin of these terms is as follows. In statistics, especially agricultural and biological, it is often necessary to investigate the distribution of a particular trait for a very large set of individuals forming a statistical team (such signs may be, for example, the protein content in wheat grain, weight of the same grain, length or body weight of some either from a group of animals, etc.). This feature is a random variable, the value of which varies from individual to individual. However, in order to get an idea of ​​the distribution of this random variable or of its most important characteristics, there is no need to examine each individual of this vast totality; It is possible to examine a certain sample of a sufficiently large volume in order to reveal the essential features of the distribution under study. That vast population from which sampling is made is called in statistics the general population. It is assumed that the number of members (individuals) 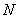in the general population is very large, and the number of members 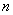in the sample is limited. When large enough 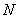It turns out that the properties of the sample (statistical) distributions and characteristics are practically independent of 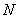; from this naturally follows a mathematical idealization, consisting in the fact that the population from which choice is made has infinite volume. At the same time, they distinguish the exact characteristics (distribution law, mathematical expectation, variance, etc.) related to the general population from the “selective” characteristics similar to them. Sample characteristics differ from the corresponding characteristics of the general population due to the limited sample size 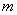; with unlimited increase 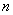naturally, all sample characteristics approach (converge in probability) to the corresponding characteristics of the general population. Often the question is, what should be the sample size 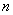so that according to the sample characteristics it was possible to judge with sufficient accuracy the unknown characteristics of the general population or the degree of accuracy with a given sample size can be judged on the characteristics of the general population. Such a methodical technique, consisting in parallel consideration of the infinite population, from which the selection is made, and limited in terms of the sample size, is quite natural in those areas of statistics where it is actually necessary to make a choice from very numerous sets of individuals. For practical tasks related to the issues of firing and arming, a different situation is much more characteristic when a limited number of experiments are performed on a random variable under investigation (or a system of random variables) in order to determine certain characteristics of this quantity, for example, when investigating the law of dispersion when shooting, a certain number of shots are made, or in order to investigate the pickup error, a series of experiments is carried out, in each of which the pickup error is recorded using a fogopulem ta, etc. At the same time, a limited number of experiments are not connected with the difficulty of registration and processing, but with the complexity and high cost of each individual experience. In this case, with a known stretch, you can also produce 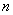experiments mentally regarded as a "sample" of some purely conventional "general population", consisting of an infinite number of possible or imaginable experiments that could be performed under these conditions. However, the artificial introduction of such a hypothetical “general population” in this formulation of the question is not caused by necessity and introduces into consideration the issue, essentially, an unnecessary element of idealization, not arising from the immediate reality of the task.

Therefore, in this course we do not use the terms “sample mean”, “sample variance”, “sample characteristics”, etc., replacing them with the terms “statistical average”, “statistical dispersion”, and “statistical characteristics”.