Event. Random events. Event probability

Event. Event probability

Each science developing a general theory of a certain range of phenomena contains a number of basic concepts on which it is based. Such, for example, in the geometry of the concept of a point, a straight line, a line; in mechanics, the concepts of force, mass, velocity, acceleration, etc. Naturally, not all basic concepts can be strictly defined, since to define a concept is to reduce it to other, more famous ones. Obviously, the process of defining some concepts through others must end somewhere, reaching the very primary concepts to which all others are reduced and which themselves are not strictly defined, but merely explained.

Such basic concepts also exist in probability theory. As the first of them, we introduce the concept of an event.

Under the "event" in the theory of probability is understood any fact that as a result of experience can occur or not happen.

A random event is a subset of the set of outcomes of a random experiment ; P

A random experiment (random test, random experience) is a mathematical model of a corresponding real experiment, the result of which cannot be accurately predicted.

Here are some examples of events:

A - the appearance of the emblem when throwing a coin;

B - the appearance of three emblems with a three-fold coin toss;

C - hitting the target when fired;

D - the appearance of an ace when removing a card from the deck;

E - object detection with one cycle of the radar survey;

F - thread breakage during the hour of operation of the loom.

Considering the above events, we see that each of them has some degree of possibility: some are greater, others less, and for some of these events we can immediately decide which of them is more and which is less possible. For example, it is immediately obvious that event A is more possible than B and D. It is impossible to make similar conclusions immediately regarding events C, E and F; for this, the conditions of experience should be clarified. One way or another, it is clear that each of these events has a certain degree of possibility. In order to quantitatively compare events with each other according to their degree of possibility, it is obviously necessary to associate with each event a certain number, which is the greater, the more event possible. We call this number the probability of an event.

Thus, we introduced into consideration the second basic concept of probability theory - the concept of probability of an event. The probability of an event is a numerical measure of the degree of objective possibility of this event.

Note that already at the very introduction of the concept of probability of an event, we associate a certain practical meaning with this concept, namely: based on experience, we consider more likely those events that occur more often; unlikely - those that almost never occur. Thus, the concept of the probability of an event is fundamentally associated with the experienced, practical concept of the frequency of an event.

Comparing with each other various events according to the degree of their possibilities, we must establish some unit of measurement. As such a unit of measurement, it is natural to accept the probability of a reliable event, i.e. such an event, which as a result of experience must necessarily occur. An example of a reliable event is a loss of no more than 6 points when throwing a single die.

If we assign a probability equal to one to a reliable event, then all other events — possible, but not reliable — will be characterized by probabilities less than one, constituting a fraction of one.

The opposite to a reliable event is an impossible event, i.e. such an event that in this experience can not occur. An example of an impossible event is the appearance of 12 points when throwing a single die. It is natural to attribute an impossible event a probability equal to zero.

Thus, the unit of measurement of probabilities is established — the probability of a reliable event — and the range of variation of the probabilities of any events — numbers from 0 to 1.

Definition, basic formulas

The classic definition of probability

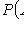
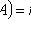
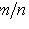
( m is the number of favorable outcomes of the experiment; n is the number of all its outcomes)

The addition theorem for probabilities of incompatible events

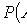
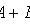
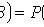
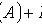
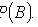
Theorem of addition of joint event probabilities

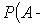
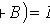
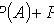
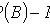
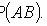
Theorem of multiplying the probability of independent events

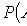
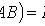
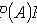
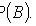
Multiplication theorem for probabilities of dependent events

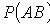
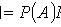
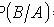
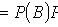
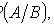
Where 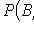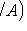- probability of event B , provided that event A has occurred.

Full probability formula

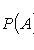
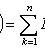
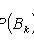
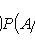
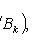
Where 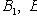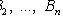- a complete group of hypotheses, i.

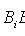
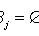
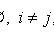
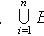
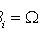
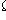
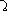( - reliable event).

Formula Bayes

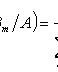
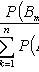
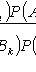
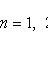
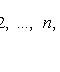
Where 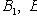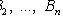- full group of hypotheses.

Repeat test

Bernoulli formula

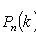
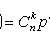
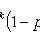
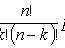
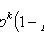
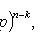
Where 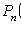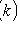- probability of occurrence of event A exactly k times with n independent tests; p is the probability of occurrence of event A at each trial.

The probability that at this event A :

1) come n times: ;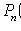

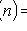
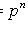2) never come: ;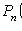

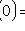
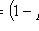
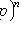3) come at least once: ;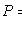

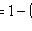
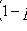
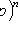4) will come no more than k times: ;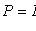

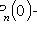
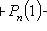
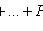
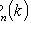5) come at least k times: .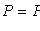

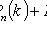
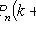
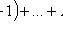
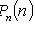Local Laplace theorem

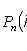
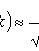
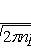
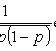
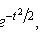
Where 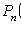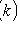- probability of occurrence of event A exactly k times with n independent tests; p is the probability of occurrence of event A at each trial; .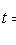

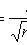
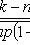
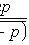Laplace integral theorem

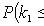
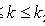
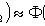
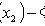
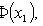
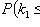
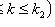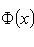
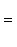
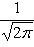
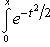
Where - the probability that in n independent trials event A appears at least k1 and not more than k2 times; 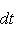- Laplace function; ; .

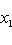
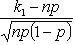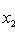
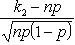Estimation of relative frequency deviation from constant probability

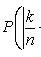
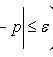
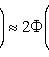
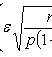
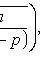
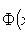
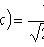
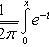
The most probable occurrence number A of event A with n independent trials

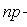
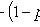
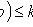
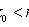
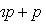
( n is the number of trials; p is the probability of an event occurring during one trial).