Lecture
The distribution law of a system (given by a distribution function or distribution density) is a complete, exhaustive characteristic of a system of several random variables. However, very often such an exhaustive characteristic cannot be applied. Sometimes the limitations of experimental material make it impossible to build the law of distribution of the system. In other cases, the study of the issue with the help of a relatively cumbersome apparatus of the laws of distribution does not justify itself due to the low demands on the accuracy of the result. Finally, in a number of problems, the approximate type of the distribution law (the normal law) is known in advance and it is only necessary to find its characteristics.
In all such cases, instead of the distribution laws, an incomplete, approximate description of a system of random variables using the minimum number of numerical characteristics is used.
The minimum number of characteristics with which the system can be characterized 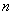 random variables
random variables 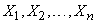 It comes down to this:
It comes down to this:
one) 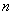 mathematical expectations
mathematical expectations
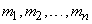 ,
,
characterizing the average values;
2) 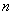 dispersions
dispersions
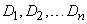 ,
,
characterizing their dispersion;
3) 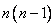 correlation moments
correlation moments
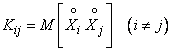 ,
,
Where
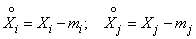 ,
,
characterizing the pairwise correlation of all quantities included in the system.
Note that the variance of each of the random variables 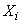 there is essentially nothing more than a special case of the correlation moment, namely the correlation moment of magnitude
there is essentially nothing more than a special case of the correlation moment, namely the correlation moment of magnitude 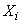 same size
same size 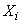 :
:
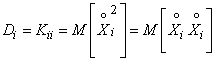 .
.
All correlation moments and variances are conveniently arranged in the form of a rectangular table (the so-called matrix):
 .
.
This table is called the correlation matrix of a system of random variables.  .
.
Obviously, not all members of the correlation matrix are different. From the definition of the correlation moment, it is clear that 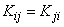 that is, the elements of the correlation matrix that are located symmetrically with respect to the main diagonal are equal. In this connection, not all the correlation matrix is often filled, but only half of it, counting from the main diagonal:
that is, the elements of the correlation matrix that are located symmetrically with respect to the main diagonal are equal. In this connection, not all the correlation matrix is often filled, but only half of it, counting from the main diagonal:
 .
.
Correlation matrix composed of elements 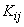 , often abbreviated as symbol
, often abbreviated as symbol 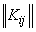 .
.
On the main diagonal of the correlation matrix are the variances of random variables. 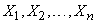 .
.
In the case when random variables 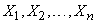 not correlated, all elements of the correlation matrix, except for the diagonal ones, are equal to zero:
not correlated, all elements of the correlation matrix, except for the diagonal ones, are equal to zero:
 .
.
Such a matrix is called diagonal.
For the sake of clarity, judgments about the correlation of random variables, irrespective of their dispersion, are often instead of a correlation matrix. 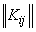 use the correlation matrix
use the correlation matrix 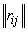 composed not of correlation moments, but of correlation coefficients:
composed not of correlation moments, but of correlation coefficients:
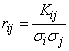 ,
,
Where
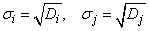 .
.
All the diagonal elements of this matrix are naturally equal to one. The normalized correlation matrix is:
 .
.
We introduce the concept of uncorrelated systems of random variables (otherwise, uncorrelated random vectors). Consider two systems of random variables:
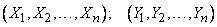
or two random vectors in 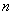 -dimensional space:
-dimensional space: 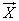 with components
with components 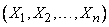 and
and 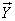 with components
with components 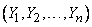 . Random vectors
. Random vectors 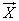 and
and 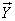 are called uncorrelated if each of the components of the vector
are called uncorrelated if each of the components of the vector 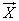 not correlated with each of the components of the vector
not correlated with each of the components of the vector 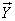 :
:
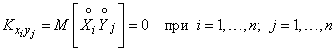 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis