Elementary event space

Elementary event space - set 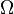all the different outcomes of a random experiment.

Element of this set 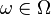called an elementary event or outcome . The space of elementary events is called discrete if the number of its elements is finite or countable. Any space of elementary events that is not discrete is called nondiscrete , and if the observed results (cannot be pronounced random events) are points of one or another numerical arithmetic or coordinate space, then the space is called continuous ( continuum ). Elementary event space 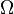together with the algebra of events 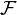and probability 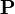forms the top three 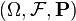called probabilistic space.

Elementary event [edit]

In probability theory, elementary events or atomic events are the outcomes of a random experiment, of which exactly one occurs in the experiment. The set of all elementary events is usually denoted. .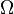

Every subset of a set 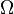Elementary events are called random events. It is said that a random event occurred as a result of the experiment. 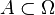if the (elementary) outcome of the experiment is an element .

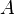In the definition of a probability space on a set of random events, a sigma-additive finite measure, called probability, is introduced.

Elementary events can have probabilities that are strictly positive, zero, indefinite, or any combination of these options. For example, any discrete probability distribution is determined by the probabilities of what may be called elementary events. In contrast, all elementary events have zero probability for continuous distribution. Mixed distributions, being neither continuous nor discrete, can contain atoms that can be thought of as elementary (i.e. event-atoms ) events with a non-zero probability. In the theory of measure in the definition of a probability space, the probability of an arbitrary elementary event could not be determined until the mathematicians saw the difference between the outcome space S and events that are of interest, and which are defined as elements of the σ-algebra of events from S.

Formally speaking, an elementary event is a subset of the outcome space of a random experiment, which consists of only one element; that is, an elementary event is still a multitude, but not the element itself. However, elementary events are usually recorded as elements, and not as sets for the purpose of simplification, when this cannot cause misunderstandings.

Examples

Examples of experiment outcome spaces, 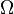and elementary events:

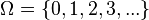• If objects are countable, and the outcome space (natural numbers), elementary events are any sets 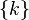where .
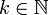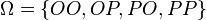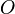• If the coin is thrown twice, , for eagle as well 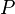for tails, then the elementary events: 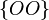, , 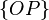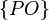and .
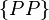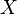• If a - these are normally distributed random variables, 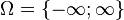, real numbers, then elementary events - any sets 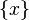where 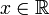. This example shows that the continuous probability distribution is not determined by the probabilities of atom events, since here the probabilities of all elementary events are zero.