The variance of a random variable is a measure of the spread of a given random variable, that is, its deviation from the mathematical expectation. Denoted by 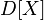 in Russian literature and
in Russian literature and 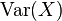 (English variance ) in foreign. The statistics often used designation
(English variance ) in foreign. The statistics often used designation 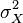 or
or 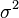 .
.
The square root of the variance is equal to 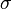 , is called standard deviation, standard deviation, or standard variation. Standard deviation is measured in the same units as the random variable itself, and variance is measured in the squares of this unit of measurement.
, is called standard deviation, standard deviation, or standard variation. Standard deviation is measured in the same units as the random variable itself, and variance is measured in the squares of this unit of measurement.
From Chebyshev's inequality, it follows that the probability that a random variable is more than k standard deviations from its expectation is less than 1 / k². For example, at least in 95% of cases, a random variable with a normal distribution is no more than two standard deviations from its average, and about 99.7% is no more than three.
Content
- 1 Definition
- 2 Notes
- 3 Properties
- 4 Example
- 5 See also
- 6 Notes
- 7 Literature
Definition [edit]
Let be 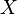 - a random variable defined on a certain probability space. Then the variance is called
- a random variable defined on a certain probability space. Then the variance is called
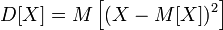
where is the symbol 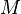 denotes the mathematical expectation [1] [2] .
denotes the mathematical expectation [1] [2] .
Remarks [edit]
- If a random variable
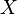 real, then, by virtue of the linearity of the expectation, the formula is valid:
real, then, by virtue of the linearity of the expectation, the formula is valid: 
- Dispersion is the second central point of a random variable;
- Dispersion can be infinite.
- Variance can be calculated using the generating function of moments.
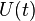 :
: 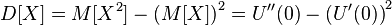
- The variance of an integer random variable can be calculated using the generating function of the sequence.
- Convenient formula for calculating the variance of a random sequence
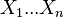 :
: 
- However, since the variance estimate is biased, to calculate it, it is necessary to additionally multiply by
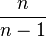 . Thus, the final formula will look like:
. Thus, the final formula will look like: 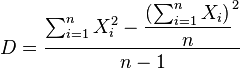
Properties [edit]
- Dispersion of any random variable is non-negative:
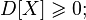
- If the variance of a random variable is finite, then of course its expectation is;
- If the random variable is constant, then its variance is zero:
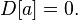 The reverse is also true: if
The reverse is also true: if 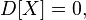 that
that 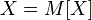 almost everywhere;
almost everywhere; - The variance of the sum of two random variables is equal to:
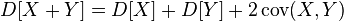 where
where 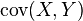 - their covariance;
- their covariance;
- For the dispersion of an arbitrary linear combination of several random variables, the following equality holds:
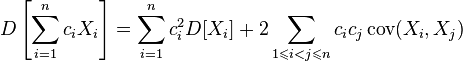 where
where 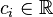 ;
;
- In particular,
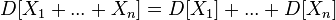 for any independent or uncorrelated random variables, since their covariances are zero;
for any independent or uncorrelated random variables, since their covariances are zero; 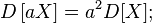
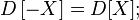
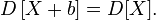
Example [edit]
Let the random variable 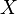 has a standard continuous uniform distribution on
has a standard continuous uniform distribution on 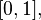 that is, its probability density is given by
that is, its probability density is given by
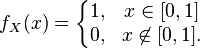
Then the mathematical expectation of a square of a random variable
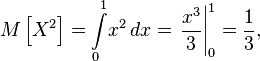
and expectation of a random variable
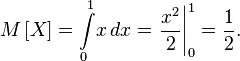
Then the variance of the random variable
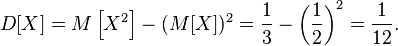
See also [edit]
- Standard deviation
- Random moments
- Covariance
- Selective dispersion
- Independence (probability theory)
- Schedasticity
- Absolute deviation
Notes [edit]
- ↑ Kolmogorov, A. N. Chapter IV. Mathematical expectations; §3. Chebyshev's inequality // Basic concepts of probability theory. - 2nd ed. - M .: Science, 1974. - p. 63-65. - 120 s.
- ↑ A. Borovkov. Chapter 4. Numerical characteristics of random variables; §five. Dispersion // Probability Theory. - 5th ed. - M .: Librokom, 2009. - p. 93-94. - 656 s.
Literature [edit]
- Gursky D., Turbina E. Mathcad for students and schoolchildren. Popular tutorial. - SPb .: Peter, 2005. - p. 340. - ISBN 5469005259.
- Orlov A. I. Variance of a random variable // Case mathematics: Probability and statistics - basic facts. - M .: MZ-Press, 2004.
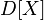 in Russian literature and
in Russian literature and 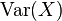 (English variance ) in foreign. The statistics often used designation
(English variance ) in foreign. The statistics often used designation 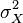 or
or 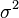 .
. 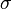 , is called standard deviation, standard deviation, or standard variation. Standard deviation is measured in the same units as the random variable itself, and variance is measured in the squares of this unit of measurement.
, is called standard deviation, standard deviation, or standard variation. Standard deviation is measured in the same units as the random variable itself, and variance is measured in the squares of this unit of measurement.  - a random variable defined on a certain probability space. Then the variance is called
- a random variable defined on a certain probability space. Then the variance is called 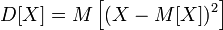
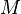 denotes the mathematical expectation [1] [2] .
denotes the mathematical expectation [1] [2] . 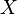 real, then, by virtue of the linearity of the expectation, the formula is valid:
real, then, by virtue of the linearity of the expectation, the formula is valid: 
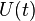 :
: 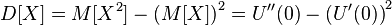
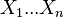 :
: 
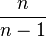 . Thus, the final formula will look like:
. Thus, the final formula will look like: 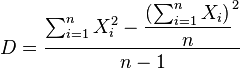
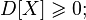
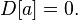 The reverse is also true: if
The reverse is also true: if 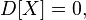 that
that 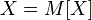 almost everywhere;
almost everywhere; 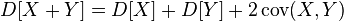 where
where 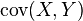 - their covariance;
- their covariance; 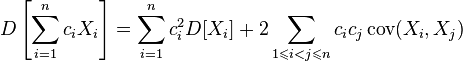 where
where 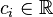 ;
; 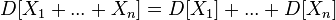 for any independent or uncorrelated random variables, since their covariances are zero;
for any independent or uncorrelated random variables, since their covariances are zero; 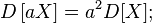
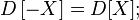
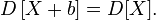
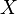 has a standard continuous uniform distribution on
has a standard continuous uniform distribution on 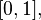 that is, its probability density is given by
that is, its probability density is given by 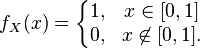
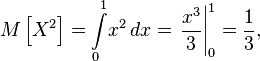
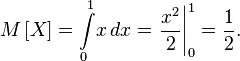
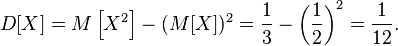
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis