You get a bonus - 1 coin for daily activity. Now you have 1 coin

13.4. The generalized Chebyshev theorem. Markov's theorem

Lecture



Chebyshev's theorem can easily be generalized to a more complicated case, namely, when the distribution law of a random variable 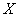13.4. The generalized Chebyshev theorem. Markovs theorem from experience to experience does not remain the same, but changes. Then instead of the arithmetic mean of the observed values ​​of the same value 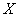13.4. The generalized Chebyshev theorem. Markovs theorem with constant expectation and variance we are dealing with arithmetic average 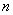13.4. The generalized Chebyshev theorem. Markovs theorem different random variables, with different mathematical expectations and variances. It turns out that even in this case, if certain conditions are met, the arithmetic average is stable and converges in probability to a certain non-random value.

The generalized Chebyshev theorem is formulated as follows. If a

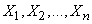13.4. The generalized Chebyshev theorem. Markovs theorem -

independent random variables with mathematical expectations

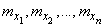
13.4. The generalized Chebyshev theorem. Markovs theorem

and dispersions

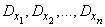
13.4. The generalized Chebyshev theorem. Markovs theorem

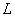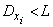
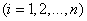and if all variances are bounded above by the same number 13.4. The generalized Chebyshev theorem. Markovs theorem :

13.4. The generalized Chebyshev theorem. Markovs theorem 13.4. The generalized Chebyshev theorem. Markovs theorem ,

then with increasing 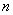13.4. The generalized Chebyshev theorem. Markovs theorem arithmetic average of observed values 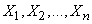13.4. The generalized Chebyshev theorem. Markovs theorem converges in probability to the arithmetic mean of their mathematical expectations.

We write this theorem as a formula. Let be 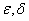13.4. The generalized Chebyshev theorem. Markovs theorem - arbitrarily small positive numbers. Then with a sufficiently large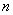 13.4. The generalized Chebyshev theorem. Markovs theorem

13.4. The generalized Chebyshev theorem. Markovs theorem . (13.4.1)

Evidence. Consider the value

13.4. The generalized Chebyshev theorem. Markovs theorem .

Her expectation is:

13.4. The generalized Chebyshev theorem. Markovs theorem ,

and the variance

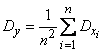13.4. The generalized Chebyshev theorem. Markovs theorem .

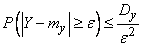Apply to value 13.4. The generalized Chebyshev theorem. Markovs theorem Chebyshev's inequality:

13.4. The generalized Chebyshev theorem. Markovs theorem ,

or

13.4. The generalized Chebyshev theorem. Markovs theorem . (13.4.2)

Replace the right side of the inequality (13.4.2) each of the quantities 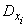13.4. The generalized Chebyshev theorem. Markovs theorem larger value 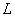13.4. The generalized Chebyshev theorem. Markovs theorem . Then the inequality will only intensify:

13.4. The generalized Chebyshev theorem. Markovs theorem .

However small 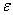13.4. The generalized Chebyshev theorem. Markovs theorem , can choose 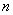13.4. The generalized Chebyshev theorem. Markovs theorem so large that inequality holds

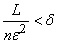13.4. The generalized Chebyshev theorem. Markovs theorem ;

then

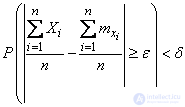13.4. The generalized Chebyshev theorem. Markovs theorem ,

whence, passing to the opposite event, we obtain the required inequality (13.4.1).

The law of large numbers can also be extended to dependent random variables. The generalization of the law of large numbers to the case of dependent random variables belongs to A. A. Markov.

Markov theorem. If there are dependent random variables 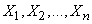13.4. The generalized Chebyshev theorem. Markovs theorem and if at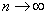 13.4. The generalized Chebyshev theorem. Markovs theorem

13.4. The generalized Chebyshev theorem. Markovs theorem ,

the arithmetic mean of the observed values ​​of random variables 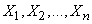13.4. The generalized Chebyshev theorem. Markovs theorem converges in probability to the arithmetic mean of their mathematical expectations. Evidence. Consider the value

13.4. The generalized Chebyshev theorem. Markovs theorem .

Obviously

13.4. The generalized Chebyshev theorem. Markovs theorem .

Apply to value 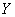13.4. The generalized Chebyshev theorem. Markovs theorem Chebyshev's inequality:

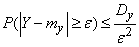13.4. The generalized Chebyshev theorem. Markovs theorem .

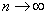
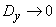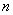
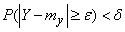As by the condition of the theorem, 13.4. The generalized Chebyshev theorem. Markovs theorem 13.4. The generalized Chebyshev theorem. Markovs theorem then at a sufficiently large 13.4. The generalized Chebyshev theorem. Markovs theorem

13.4. The generalized Chebyshev theorem. Markovs theorem ,

or, moving to the opposite event,

13.4. The generalized Chebyshev theorem. Markovs theorem ,

Q.E.D.

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Probability theory. Mathematical Statistics and Stochastic Analysis

Terms: Probability theory. Mathematical Statistics and Stochastic Analysis