Lecture
Probability function 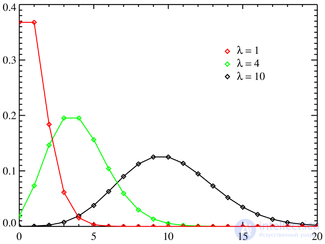 | |
Distribution function 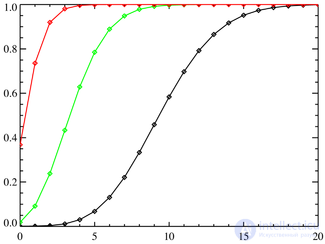 | |
| Designation | 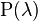 |
| Options | 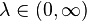 |
| Carrier | 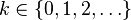 |
| Probability function | 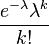 |
| Distribution function | 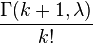 |
| Expected value | 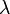 |
| Median | 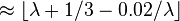 |
| Fashion | 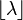 |
| Dispersion | 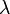 |
| Asymmetry coefficient | 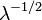 |
| Coefficient of kurtosis | 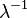 |
| Informational entropy | 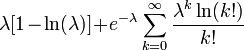 |
| Generating function of moments | 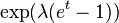 |
| Characteristic function | 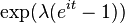 |
The Poisson distribution is a probability distribution of a discrete type, models a random variable representing the number of events that occurred in a fixed time, provided that these events occur with a certain fixed average intensity and independently of each other.
Poisson distribution plays a key role in queuing theory.
Choose a fixed number 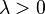 and define a discrete distribution defined by the following probability function:
and define a discrete distribution defined by the following probability function:
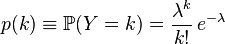 ,
, Where
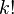 denotes factorial numbers
denotes factorial numbers 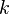 ,
, 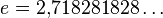 - the basis of natural logarithm.
- the basis of natural logarithm. The fact that the random variable 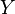 has a Poisson distribution with the parameter
has a Poisson distribution with the parameter 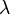 recorded:
recorded: 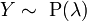 .
.
The generating Poisson distribution moment function has the form:
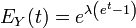 ,
, from where
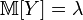 ,
, 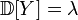 .
. For factorial distribution points, the general formula is valid:
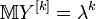 ,
, Where 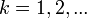
And since the moments and factorial moments are linearly related, it is often for the Poisson distribution that the factorial moments are investigated, from which, if necessary, ordinary moments can be derived.
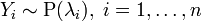 . Then
. Then 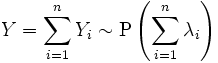 .
. 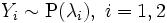 and
and 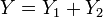 . Then the conditional distribution
. Then the conditional distribution 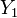 provided that
provided that 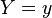 , binomially. More accurately:
, binomially. More accurately: 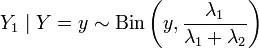 .
. Quite often in probability theory it is not the Poisson distribution itself that is considered, but a sequence of distributions that are asymptotically equal to it. More formally, consider a sequence of random variables. 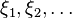 , taking integer values, such that for any
, taking integer values, such that for any 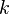 done
done 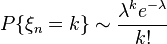 at
at  .
.
The simplest example is the case when 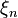 has a binomial distribution with probability of success
has a binomial distribution with probability of success  in each of
in each of 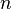 tests.
tests.
Consider a sequence of random variables 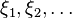 that accept integer non-negative values. If a
that accept integer non-negative values. If a 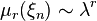 at
at 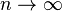 and any fixed
and any fixed  (Where
(Where 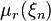 -
-  factor factor), then for all
factor factor), then for all 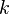 at
at 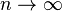 done
done 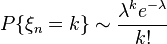 .
.
To begin with, we prove the general formula for calculating the probability of a specific value of a random variable appearing through factorial moments. Let for some 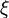 all are known
all are known 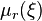 and
and 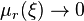 at
at 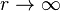 . Then
. Then
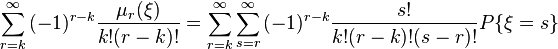
By changing the summation order, this expression can be converted to
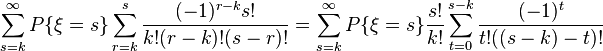
Further, from the known formula 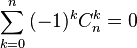 we get that
we get that 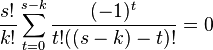 at
at 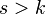 the same expression degenerates into
the same expression degenerates into 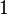 at
at 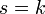 .
.
Thus, it is proved that 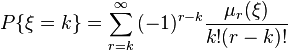
According to the lemma and the conditions of the theorem, 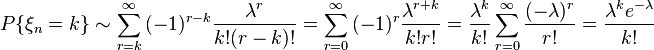 at
at 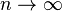 .
.
QED
As an example of a non-trivial consequence of this theorem, for example, the asymptotic tendency to 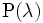 the distribution of the number of isolated edges (two-vertex connected components) in a random
the distribution of the number of isolated edges (two-vertex connected components) in a random 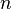 -vertex graph, where each of the edges is included in the graph with probability
-vertex graph, where each of the edges is included in the graph with probability 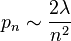 . [one]
. [one]
The work of Poisson "Studies on the probability of sentences in criminal and civil cases" was published in 1837. [2] [3] Examples of other situations that can be modeled using this distribution: equipment breakdowns, the duration of repair work performed by a stably working employee, a printing error, the growth of a colony of bacteria in a Petri dish, defects in a long ribbon or chain, radiation counter pulses et al. [4]
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis