Lecture
One of the important practical problems arising in the study of issues of shooting and bombing is the task of processing the results of experimental shooting (bombing).
Here we will distinguish between two cases: the firing of shock projectiles and the firing of remote projectiles.
When firing assault projectiles, dispersion is characterized by the law of distribution of a system of two random variables: the abscissas and the ordinates of the hit point on a certain plane (real or imaginary). When firing remote projectiles dispersion is spatial in nature and is described by the law of distribution of the system of three coordinates of the point of rupture of the projectile.
We first consider the problem of processing the firing of shock shells. Let produced 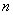 independent shots on some flat target and coordinates are recorded
independent shots on some flat target and coordinates are recorded 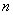 hit points (Fig. 14.7.1):
hit points (Fig. 14.7.1):
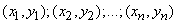 .
.
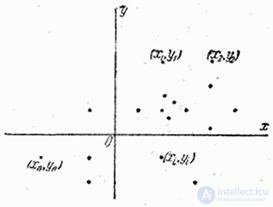
Fig. 14.7.1.
Assuming that the distribution law of the system 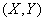 normal, you want to find estimates for its parameters: the coordinates of the center of dispersion
normal, you want to find estimates for its parameters: the coordinates of the center of dispersion 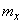 ,
, 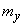 corner
corner 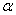 determining the direction of the main dispersion axes
determining the direction of the main dispersion axes 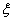 ,
, 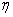 and main shots
and main shots 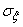 ,
, 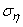 .
.
We begin by considering the simplest case when the direction of the main axes of dispersion is known in advance. This case is often found in practice, since usually the direction of the main dispersion axes is determined by the shooting conditions themselves (for example, during bombing, the direction of flight and perpendicular to it; in aerial shooting, the direction of transverse velocity of the target and perpendicular to it, etc.). In this case, the task of handling firing is greatly simplified. Knowing in advance at least tentatively the direction of the main axes, one can choose coordinate axes parallel to them; in such a coordinate system, the abscissa and ordinate of the point of entry are independent random variables, and their distribution law is determined by only four parameters: the coordinates of the center of dispersion and the main standard quadratic deviations 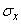 ,
, 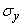 . Estimates for these parameters are determined by the formulas
. Estimates for these parameters are determined by the formulas
 (14.7.1)
(14.7.1)
Let us consider a more complicated case when the direction of the main axes of dispersion is not known in advance and must also be determined from experience. In this case, estimates of all five parameters should be determined: the coordinates of the center of dispersion 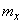 ,
, 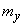 corner
corner 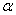 and principal mean square deviations
and principal mean square deviations 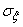 ,
, 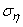 (fig. 14.7.2).
(fig. 14.7.2).
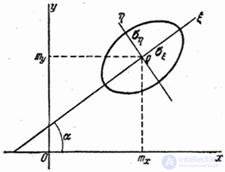
Fig. 14.7.2.
Estimates for the coordinates of the center of dispersion in this case are determined in the same way as in the previous case, using the formulas
 ;
;  . (14.7.2)
. (14.7.2)
Let us turn to the evaluation of the angle 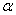 . Suppose that the directions of the main axes of dispersion are known, and draw through the point
. Suppose that the directions of the main axes of dispersion are known, and draw through the point 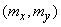 main axles
main axles  ,
,  (fig. 14.7.2). In system
(fig. 14.7.2). In system 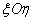 coordinates of a random point
coordinates of a random point 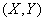 will be:
will be:
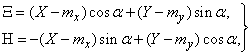
or
 (14.7.3)
(14.7.3)
Obviously the magnitude 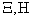 will have a mathematical expectation of zero:
will have a mathematical expectation of zero:
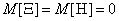 .
.
Since the axes 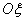 ,
, 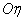 - main scattering axes, magnitudes
- main scattering axes, magnitudes 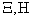 are independent. But for quantities subject to normal law, independence is equivalent to uncorrelatedness; therefore, we only need to find such an angle
are independent. But for quantities subject to normal law, independence is equivalent to uncorrelatedness; therefore, we only need to find such an angle 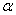 at which values
at which values 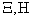 not correlated. This value determines the direction of the main axes of dispersion.
not correlated. This value determines the direction of the main axes of dispersion.
Calculate the correlation moment values 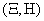 . Multiplying equalities (14.7.3) and applying to the product of their mathematical expectation operation, we get:
. Multiplying equalities (14.7.3) and applying to the product of their mathematical expectation operation, we get:
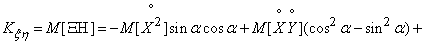
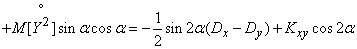 .
.
Equating this expression to zero and dividing both parts by 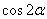 , we have:
, we have:
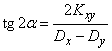 . (14.7.4)
. (14.7.4)
Equation (14.7.4) gives two angle values 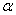 :
: 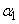 and
and 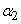 differing by
differing by 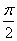 . These two angles determine the directions of the main axes of dispersion.
. These two angles determine the directions of the main axes of dispersion.
Replacing in equality (14.7.4) 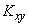 ,
, 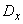 ,
, 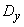 their estimates, we obtain the estimate for the angle
their estimates, we obtain the estimate for the angle 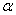 :
:
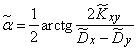 .
.
Find the estimates for the main standard quadratic deviations. 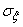 ,
, 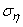 . For this we find the variances
. For this we find the variances 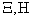 given by formulas (14.7.3), according to the theorem on the dispersion of a linear function:
given by formulas (14.7.3), according to the theorem on the dispersion of a linear function:
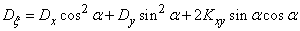 ;
;
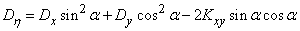 ,
,
where do we find the estimates for the main variances:
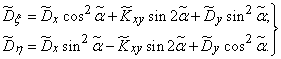 (14.7.5)
(14.7.5)
Estimates for the main standard deviations are expressed by the formulas:
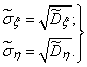 (14.7.6)
(14.7.6)
Let us write separately a full summary of the formulas for the treatment of firing at a flat target in the case when the direction of the main axes of dispersion is not known in advance. Estimates of the desired parameters are determined by the formulas:
 (14.7.7)
(14.7.7)
Where
 (14.7.8)
(14.7.8)
In conclusion, it should be noted that it makes sense to take up firing on the full formulas (14.7.7) only when the number of experiments is large enough (of the order of many dozen; only in this case is the angle 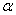 can be evaluated with reasonable accuracy. With a small number of observations value
can be evaluated with reasonable accuracy. With a small number of observations value 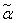 , obtained by processing, is largely random.
, obtained by processing, is largely random.
The task of firing remote projectiles, we consider here only in the simplest case, when the direction of the main axes of dispersion (at least tentatively) is known in advance. As a rule, the tasks of processing experiments occurring in the practice of firing with remote projectiles are of this type. Then you can choose the coordinate axes parallel to the main axes of dispersion and consider the three coordinates of the point of rupture of the projectile as independent random variables.
Let the result 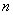 independent shots recorded coordinates
independent shots recorded coordinates 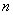 distance points of remote projectiles
distance points of remote projectiles
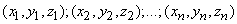
in coordinate system with axes parallel to the main scatter axes. Estimates for the parameters of the normal law are determined by the formulas:
 (14.7.9)
(14.7.9)
We will not stop on solving the problem of shooting with remote projectiles in the case when the directions of the main scattering axes are not known beforehand, since in practice this problem is relatively rare.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis