2.5. Almost impossible and almost reliable events. The principle of practical universality

In n 2.2 we got acquainted with the concepts of an impossible and reliable event. The probability of an impossible event, equal to zero, and the probability of a reliable event, equal to one, occupy extreme positions on the probability scale.

In practice, one often has to deal not with impossible and reliable events, but with so-called “almost impossible” and “almost reliable” events.

A practically impossible event is an event whose probability is not exactly zero, but very close to zero.

Consider, for example, the following experience: 32 letters of the split alphabet are mixed together; One card is removed, the letter shown on it is recorded, after which the removed card is returned and the cards are shuffled. This experience is done 25 times. Consider event A, which consists in the fact that after 25 extracts we will write the first line of "Eugene Onegin":

"My uncle of the most honest rules."

Such an event is not logically impossible; can calculate his probability which is equal 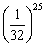; but in view of the fact that the probability of an event A is negligible, it can be considered practically impossible.

A practically reliable event is an event whose probability is not exactly equal to one, but very close to one.

If any event 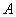in this experience is almost impossible, the opposite event 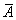failing event 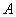It will be almost reliable. Thus, from the point of view of the theory of probabilities, it is all the same which events to talk about: practically impossible or practically reliable, as they always accompany each other.

Practically impossible and practically reliable events play a large role in probability theory; All practical application of this science is based on them.

In fact, if we know that the probability of an event in this experience is 0.3, this still does not allow us to predict the result of the experiment. But if the probability of an event in a given experiment is negligible or, conversely, very close to unity, this allows us to predict the result of the experiment; in the first case, we will not expect the event 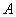; in the second case, we will expect it with sufficient reason. With this prediction, we are guided by the so-called principle of practical certainty, which can be formulated as follows.

If the probability of some event 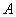in this experience 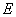is very small, then you can be almost certain that with a one-time experience 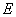event 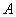will not happen.

In other words, if the probability of an event 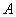in this experience is very small, then, starting to perform the experience, you can organize your behavior as if this event is impossible at all, that is, not counting on his appearance at all.

In everyday life, we continuously unconsciously use the principle of practical confidence. For example, going on a journey by rail, we all organize our behavior, disregarding the possibility of a train accident, although there is some very small probability of such an event.

The principle of practical certainty cannot be proved by mathematical means; it is confirmed by all the practical experience of mankind.

The question of how small the probability of an event should be so that it can be considered practically impossible is beyond the scope of mathematical theory and in each case is solved from practical considerations in accordance with the importance that the desired result of experience has for us.

For example, if the probability of failure of a fuse when fired is 0.01, we can still reconcile with this and consider the failure of a fuse to be an almost impossible event. On the contrary, if the probability of a parachute failure during a jump is also equal to 0.01, we obviously cannot consider this failure as an almost impossible event and should strive for greater reliability of the parachute operation.

One of the most important tasks of probability theory is the identification of practically impossible (or practically reliable) events, which make it possible to predict the result of experience, and the identification of conditions under which certain events become almost impossible (reliable). There are a number of theorems of probability theory - the so-called limit theorems, which establish the existence of events that become almost impossible (reliable) with an increase in the number of experiments or with an increase in the number of random variables involved in the problem. An example of such a limit theorem is the already formulated Bernoulli theorem (the simplest form of the law of large numbers). According to the Bernoulli theorem, with a large number of experiments, an event consisting in the fact that the difference between the frequency of the event and its probability is arbitrarily small, becomes almost reliable.

Along with practically impossible (reliable) events that allow one to predict the outcome of an experiment with confidence, despite the presence of randomness, random variables play an important role in probability theory, which, although they are random, have such minor fluctuations that they can practically be considered if not random. An example of such an “almost non-random” value is the frequency of an event with a large number of experiments. Although this value is random, with a large number of experiments, it can practically fluctuate only within very narrow limits near the probability of an event.

Such “almost non-random” values ​​make it possible to predict the numerical result of experience, despite the presence of elements of randomness in it, operating with this result as confidently as we operate with data that is delivered by conventional methods of the exact sciences.