Lecture
Let random point 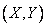 on the plane is subject to normal law
on the plane is subject to normal law
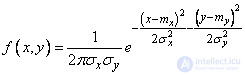 (9.3.1)
(9.3.1)
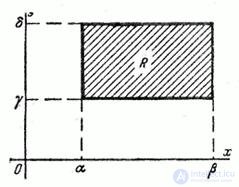
Fig. 9.3.1.
In this case, the main axes of dispersion are parallel to the coordinate axes and the values  and
and 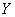 are independent.
are independent.
It is required to calculate the probability of hitting a random point. 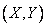 into a rectangle
into a rectangle  whose sides are parallel to the coordinate axes
whose sides are parallel to the coordinate axes 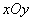 , and, therefore, the main axes of dispersion (Fig. 9.3.1). According to the general formula (8.3.4) we have:
, and, therefore, the main axes of dispersion (Fig. 9.3.1). According to the general formula (8.3.4) we have:
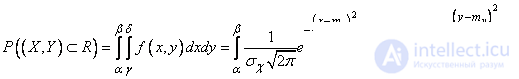 .
.
whence, applying the formula (6.3.3) for the probability of hitting the site, we find:
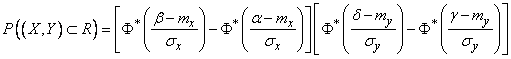 , (9.3.2)
, (9.3.2)
Where 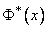 - normal distribution function.
- normal distribution function.
If the normal law on a plane is given in canonical form, then 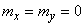 , and the formula (9.3.2) takes the form
, and the formula (9.3.2) takes the form
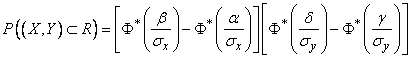 . (9.3.3)
. (9.3.3)
If the sides of the rectangle are not parallel to the coordinate axes, then formulas (9.3.2) and (9.3.3) are no longer applicable. Only with circular scattering, the probability of hitting a rectangle of any orientation is calculated by the formula (9.3.2) or (9.3.3).
Formulas (9.3.2) and (9.3.3) are widely used in calculating the probabilities of hitting the target: rectangular, close to rectangular, composed of rectangles, or approximately replaced by those.
Example. Shooting from a plane at a rectangular shield size 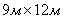 lying on the ground horizontally. Main probable deviations: in the longitudinal direction
lying on the ground horizontally. Main probable deviations: in the longitudinal direction 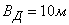 in the lateral direction
in the lateral direction 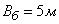 . Aiming - in the center of the target, approach - along the target. Due to the discrepancy between the shooting range and the actual shooting range, the average point of impact shifts towards undershoot by
. Aiming - in the center of the target, approach - along the target. Due to the discrepancy between the shooting range and the actual shooting range, the average point of impact shifts towards undershoot by 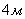 . Find the probability of hitting the target with one shot.
. Find the probability of hitting the target with one shot.

Fig. 9.3.2.
Decision. In the drawing (fig. 9.3.2) we put the target, the aiming point (etc.) and the center of dispersion (c. P.). Through ts.r. draw the main axis of dispersion: in the direction of flight and perpendicular to it.
Let's go from the main probable deviations 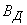 and
and 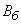 to the main mean squares:
to the main mean squares:
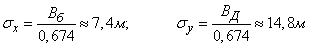 .
.
By the formula (9.3.3) we have:
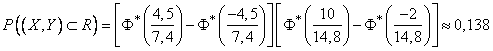
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis