Lecture
The probability distribution is a law that describes the range of values of a random variable and the probability of their outcome (appearance).
Definition 1. Let probability space be given 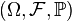 and a random variable is defined on it
and a random variable is defined on it 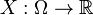 . In particular, by definition,
. In particular, by definition, 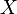 is a measurable mapping of measurable space
is a measurable mapping of measurable space 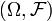 in a measurable space
in a measurable space 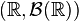 where
where 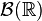 denotes a Borel sigma-algebra on
denotes a Borel sigma-algebra on 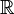 . Then a random variable
. Then a random variable 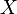 induces a probability measure
induces a probability measure 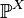 on
on 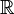 in the following way:
in the following way:

Measure 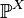 called a random variable distribution
called a random variable distribution 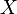 . In other words,
. In other words, 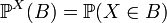 , in this way
, in this way 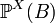 sets the probability that a random variable
sets the probability that a random variable 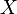 falls into the set
falls into the set 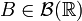 .
.
Definition 2. Function  is called the (cumulative) distribution function of a random variable
is called the (cumulative) distribution function of a random variable 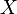 . From the properties of probability follows
. From the properties of probability follows
Theorem 1. The distribution function 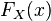 any random variable satisfies the following three properties:
any random variable satisfies the following three properties:
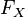 - non-decreasing function;
- non-decreasing function; 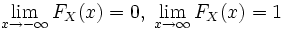 ;
; 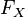 continuous on the right.
continuous on the right. From the fact that a Borel sigma-algebra on a real line is generated by a family of intervals of the form 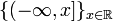 implies
implies
Theorem 2. Any function 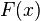 satisfying the three properties listed above is a distribution function for some distribution
satisfying the three properties listed above is a distribution function for some distribution 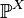 .
.
For probability distributions with certain properties, there are more convenient ways to set it.
Definition 3. A random variable is called simple or discrete if it takes no more than a countable number of values. I.e 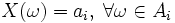 where
where 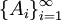 - splitting
- splitting 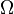 .
.
The distribution of a simple random variable is then defined by definition: 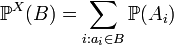 . Enter the designation
. Enter the designation 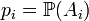 can set function
can set function 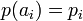 . It's obvious that
. It's obvious that 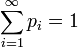 . Using countable additivity
. Using countable additivity 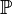 it is easy to show that this function uniquely determines the distribution
it is easy to show that this function uniquely determines the distribution 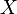 .
.
Definition 4. Function 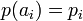 where
where 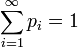 often referred to as a discrete distribution .
often referred to as a discrete distribution .
Example 1. Let function 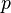 set in such a way that
set in such a way that 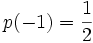 and
and 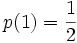 . This function sets the distribution of the random variable.
. This function sets the distribution of the random variable.  , for which
, for which 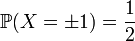 (Bernoulli distribution).
(Bernoulli distribution).
Theorem 3. Discrete distribution has the following properties:
one. 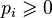 ;
;
2 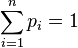 .
.
A continuous distribution is a distribution that does not have atoms.
Absolutely continuous are the distributions having a probability density. The cumulative function of such distributions is absolutely continuous in the sense of Lebesgue.
Definition 5. The distribution of a random variable. 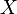 called absolutely continuous if there is a non-negative function
called absolutely continuous if there is a non-negative function 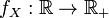 such that
such that 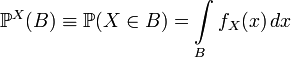 . Function
. Function 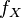 then called the distribution density of a random variable
then called the distribution density of a random variable 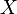 .
.
Example 2. Let 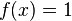 when
when 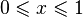 and
and 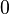 - otherwise. Then
- otherwise. Then 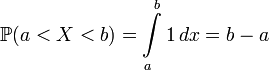 , if a
, if a  .
.
Obviously, for any density distribution 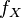 true equality
true equality 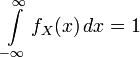 . True and reverse
. True and reverse
Theorem 4. If the function 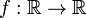 such that:
such that:
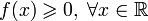 ;
; 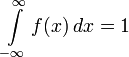 ,
, then there is a distribution 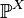 such that
such that 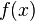 is its density.
is its density.
Simply applying the Newton-Leibniz formula leads to a simple relationship between the cumulative function and the density of an absolutely continuous distribution.
Theorem 5. If 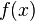 - continuous distribution density, and
- continuous distribution density, and 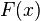 - its cumulative function, then
- its cumulative function, then
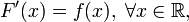
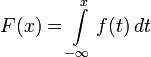 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis