Lecture
Knowing the distribution law of a system of two random variables, one can always determine the distribution laws of individual quantities included in the system. AT  we have already derived expressions for the distribution functions of the individual quantities entering the system through the distribution function of the system, namely, we have shown that
we have already derived expressions for the distribution functions of the individual quantities entering the system through the distribution function of the system, namely, we have shown that
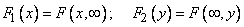 (8.4.1)
(8.4.1)
We now express the distribution density of each of the quantities included in the system, through the distribution density of the system. Using formula (8.3.5), which expresses the distribution function in terms of the distribution density, we write:
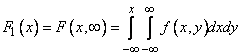 ,
,
from where differentiating by 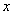 , we obtain the expression for the distribution density of
, we obtain the expression for the distribution density of 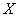 :
:
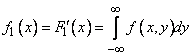 (8.4.2)
(8.4.2)
Similarly
 (3.4.3)
(3.4.3)
Thus, in order to obtain the distribution density of one of the quantities included in the system, it is necessary to integrate the distribution density of the system in infinite limits over the argument corresponding to another random variable.
Formulas (8.4.1), (8.4.2) and (8.4.3) make it possible, knowing the law of distribution of the system (specified as a distribution function or density of distribution), to find the laws of distribution of individual quantities in the system. Naturally, the question arises about the inverse problem: is it possible according to the laws of the distribution of individual quantities in. system, restore the law of distribution of the system? It turns out that in the general case this cannot be done: knowing only the laws of the distribution of individual quantities entering the system, it is not always possible to find the law of distribution of the system. In order to exhaustively characterize the system, it is not enough to know the distribution of each of the quantities included in the system; you also need to know the relationship between the quantities included in the system. This dependence can be characterized using the so-called conditional distribution laws.
Conditional law of size distribution 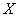 entering the system
entering the system 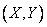 , is called its distribution law, calculated under the condition that another random variable
, is called its distribution law, calculated under the condition that another random variable 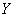 took a certain meaning
took a certain meaning 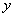 .
.
The conditional distribution law can be specified both by the distribution function and by density. The conditional distribution function is denoted by 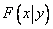 conditional distribution density
conditional distribution density 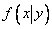 . Since systems of continuous quantities are of fundamental practical importance, we will limit ourselves in this course to the consideration of conditional laws given by the density of distribution.
. Since systems of continuous quantities are of fundamental practical importance, we will limit ourselves in this course to the consideration of conditional laws given by the density of distribution.
To clarify the concept of the conditional distribution law, consider an example. Random variable system 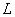 and
and 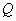 represents the length and weight of the fragment of the projectile. Let us be interested in the length of the fragment
represents the length and weight of the fragment of the projectile. Let us be interested in the length of the fragment 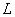 whatever its weight; it is a random variable subject to the distribution law with density
whatever its weight; it is a random variable subject to the distribution law with density 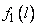 . We can investigate this law of distribution by examining all the fragments without exception and evaluating them only by length;
. We can investigate this law of distribution by examining all the fragments without exception and evaluating them only by length; 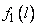 there is an unconditional law of the distribution of the length of the fragment. However, we may be interested in the law of distribution of the length of a fragment of a well-defined weight, for example, 10 g. In order to determine it, we will not examine all the fragments, but only a certain weight group in which the weight is approximately equal to 10 g, and obtain the conditional law of length distribution shrapnel weighing 10 g with a density
there is an unconditional law of the distribution of the length of the fragment. However, we may be interested in the law of distribution of the length of a fragment of a well-defined weight, for example, 10 g. In order to determine it, we will not examine all the fragments, but only a certain weight group in which the weight is approximately equal to 10 g, and obtain the conditional law of length distribution shrapnel weighing 10 g with a density 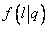 at
at 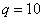 . This conditional distribution law is generally different from unconditional
. This conditional distribution law is generally different from unconditional 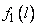 ; obviously, heavier fragments should, on average, have a longer length; therefore, the conditional law of length distribution depends significantly on the weight
; obviously, heavier fragments should, on average, have a longer length; therefore, the conditional law of length distribution depends significantly on the weight 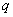 .
.
Knowing the distribution law of one of the quantities included in the system, and the conditional distribution law of the second, we can make up the distribution law of the system. We derive a formula expressing this relation for continuous random variables. To do this, we use the concept of the element of probability. Consider adjacent to the point  elementary rectangle
elementary rectangle 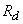 with the parties
with the parties 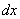 ,
, 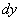 (fig. 8.4.1). The probability of hitting this rectangle is an element of probability
(fig. 8.4.1). The probability of hitting this rectangle is an element of probability 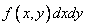 - equal to the probability of simultaneous hitting a random point
- equal to the probability of simultaneous hitting a random point 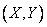 in elementary strip I, based on the segment
in elementary strip I, based on the segment 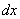 and in lane II, bearing on the segment
and in lane II, bearing on the segment 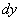 :
:
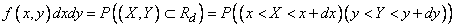 .
.
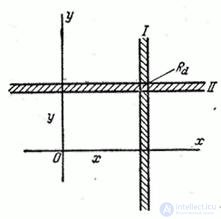
Fig.8.4.1
The probability of the product of these two events, according to the probability multiplication theorem, is equal to the probability of falling into elementary lane I multiplied by the conditional probability of falling into elementary lane II, calculated under the condition that the first event took place. This condition in the limit is equivalent to the condition 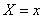 , Consequently,
, Consequently,
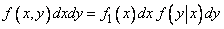 ,
,
from where
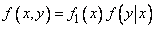 , (8.4.4)
, (8.4.4)
those. the distribution density of a system of two quantities is equal to the distribution density of one of the quantities included in the system multiplied by the conditional distribution density of another quantity, calculated under the condition that the first quantity has taken the specified value.
Formula (8.4.4) is often called the theorem of multiplication of the distribution laws. This theorem in the scheme of random variables is similar to the theorem on multiplication of probabilities in the scheme of events.
Obviously, the formula (8.4.4) can be given a different form, if you specify a value not values 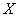 , and values
, and values 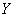 :
:
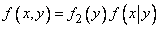 . (8.4.5)
. (8.4.5)
Solving formulas (8.4.4) and (8.4.5) with respect to 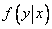 and
and 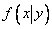 , we obtain the expression of conditional laws of distribution through unconditional:
, we obtain the expression of conditional laws of distribution through unconditional:
 (8.4.6)
(8.4.6)
or by applying formulas (8.4.2) and (8.4.3),
 (8.4.7)
(8.4.7)
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis