Lecture
In the previous 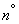 The question of the transformation of a stationary random function by a stationary linear system was considered, and simple mathematical methods for solving this problem were obtained. The transformation of a random function was reduced to the simplest transformation (multiplied by the square of the frequency response module) of a single function: spectral density. Such simplicity of the spectral theory of stationary random processes makes it an indispensable device in the study of linear dynamic systems operating in the presence of random perturbations (noise).
The question of the transformation of a stationary random function by a stationary linear system was considered, and simple mathematical methods for solving this problem were obtained. The transformation of a random function was reduced to the simplest transformation (multiplied by the square of the frequency response module) of a single function: spectral density. Such simplicity of the spectral theory of stationary random processes makes it an indispensable device in the study of linear dynamic systems operating in the presence of random perturbations (noise).
Usually, when solving practical problems, we are not interested in the correlation function itself. 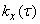 at the output of the system, and the variance associated with it
at the output of the system, and the variance associated with it
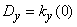 ,
,
which characterizes system errors caused by random perturbations arriving at it, and in many cases can serve as a criterion for the accuracy of the system.
In the study of dynamic systems using the theory of random functions, two types of problems are solved, which can be called "direct" and "inverse."
The direct challenge is as follows. The given linear dynamic system is analyzed with well-defined parameters, whose operation is described by a linear differential equation:
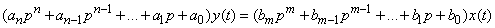 . (17.6.1)
. (17.6.1)
It is required to investigate the accuracy of the system in the presence of stationary random effects at its input - the so-called “stationary interference”. To do this, first of all, the random interference is investigated, its correlation function and spectral composition are determined. Further, by the methods described above, the spectrum and the dispersion of a random function are found at the output of the system. The variance at the output obviously depends on both the characteristics of the random action at the input and the coefficients of the equation. Solving such a problem, it is possible to estimate the accuracy of a given system in conditions of various kinds of interference.
The inverse problem is to choose the coefficients of equation (17.6.1) so that, for a given spectral composition, the disturbances of the error at the output of the system are minimal. Given the characteristics of the random function (noise) at the system input, the dispersion at the output depends on the whole set of coefficients of the equation:
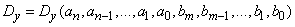 .
.
The coefficients of the equation depend on the design parameters of the system, and some of them can be controlled within sufficiently wide limits when designing the system. The problem of choosing rational values of these parameters can be solved based on the requirement that the variance 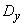 was minimal.
was minimal.
It should be noted that in practice it is often not possible to fully satisfy this requirement. Indeed, the expressions derived by us for the correlation function and the variance at the output of the system are valid only for time values 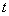 sufficiently distant from the beginning of the random process, when all the transient processes in the system, associated with its free oscillations, have already faded away. In fact, it is often necessary to use linear dynamic systems (sights, computing systems, tracking systems, etc.) in a limited area of time; at the same time, the decay rate of transients in the system substantially depends on its design parameters, i.e., on the same coefficients of equation (17.6.1). If we choose these coefficients so that they reduce the output variance to a minimum (for sufficiently distant time points), this, as a rule, leads to the fact that other errors appear at the system output due to the fact that transients in the system have not yet managed to fade. These errors are usually referred to as dynamic errors.
sufficiently distant from the beginning of the random process, when all the transient processes in the system, associated with its free oscillations, have already faded away. In fact, it is often necessary to use linear dynamic systems (sights, computing systems, tracking systems, etc.) in a limited area of time; at the same time, the decay rate of transients in the system substantially depends on its design parameters, i.e., on the same coefficients of equation (17.6.1). If we choose these coefficients so that they reduce the output variance to a minimum (for sufficiently distant time points), this, as a rule, leads to the fact that other errors appear at the system output due to the fact that transients in the system have not yet managed to fade. These errors are usually referred to as dynamic errors.
Due to the time constraints of the application of linear systems and the presence of dynamic errors in practice, one usually has to solve the problem of a rational choice of system parameters not on the pure principle of minimum dispersion, but taking into account dynamic errors. A rational solution of the problem is found as a compromise, in which, on the one hand, the variance at the output of the system is rather small, on the other hand, the dynamic errors are not too large.
In the case when optimal parameters of the system are sought, taking into account both the variance and systematic dynamic errors, the second initial moment is often chosen as the criterion for the accuracy of the system 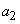 system output:
system output:
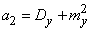 , (17.6.2)
, (17.6.2)
Where 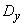 - dispersion
- dispersion 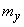 - systematic error at the output of the system. In this case, the system parameters are chosen so that they convert to a minimum value
- systematic error at the output of the system. In this case, the system parameters are chosen so that they convert to a minimum value 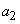 .
.
Sometimes, as a criterion for estimating a system, it is not any variance and not a second starting point that is chosen, but some other value related to the purpose of the system. For example, in the study of sighting devices and control systems intended for firing, the choice of their parameters is often appropriate on the basis of the maximum probability of hitting the target.
Let us mention one more typical problem connected with the rational construction of dynamical systems. So far, we have considered only the problem of the rational choice of the coefficients of equation (17.6.1), the very same kind of equation was considered given. When solving problems associated with the so-called synthesis of dynamic systems, the problem is posed more broadly. In particular, it raises the question of the rational choice of the very type of the equation or, even more broadly, the problem of determining the optimal operator of a dynamical system. Such problems are now successfully solved by methods of the theory of random functions.
In solving practical problems associated with the analysis and synthesis of dynamic systems, it is often not possible to limit oneself to the range of stationary random processes and the spectral theory apparatus relating to it. However, in some cases, somewhat modifying this apparatus, you can apply it to non-stationary processes. In practice, so-called “quasistationary” random functions and “quasistationary” dynamical systems are often encountered; they are characterized by the fact that changes in the characteristics of random functions and system parameters over time proceed relatively slowly. For such random processes, V. S. Pugachev developed a method that differs little from the spectral one in structure, but is applicable in a wider range of conditions.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis