Lecture
Linear regression is a regression model used in statistics for the dependence of one (explicable, dependent) variable y on another or several other variables (factors, regressors, independent variables) x with a linear dependence function.
The linear regression model is often used and most studied in econometrics. Namely, the properties of parameter estimates obtained by various methods under the assumptions about the probability characteristics of factors and random model errors are studied. The limiting (asymptotic) properties of estimates of nonlinear models are also derived based on the approximation of the latter by linear models. It should be noted that, from an econometric point of view, linearity in parameters is more important than linearity in model factors.
Regression model
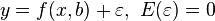 ,
,
Where 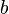 - model parameters,
- model parameters,  - random model error, called linear regression, if the regression function
- random model error, called linear regression, if the regression function 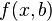 has the appearance
has the appearance
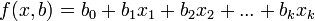 ,
,
Where 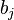 - regression parameters (coefficients),
- regression parameters (coefficients), 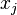 - regressors (model factors), k - number of model factors.
- regressors (model factors), k - number of model factors.
The linear regression coefficients show the rate of change of the dependent variable for a given factor, with other factors fixed (in the linear model this rate is constant):
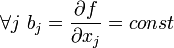
Parameter 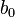 at which there are no factors, is often called a constant . Formally, this is the value of the function with zero value of all factors. For analytical purposes, it is convenient to assume that a constant is a parameter with a "factor" equal to 1 (or another arbitrary constant, therefore this factor is also called a constant). In this case, if you re-number the factors and parameters of the original model with this in mind (leaving the designation of the total number of factors - k), then the linear regression function can be written in the following form, which formally does not contain a constant:
at which there are no factors, is often called a constant . Formally, this is the value of the function with zero value of all factors. For analytical purposes, it is convenient to assume that a constant is a parameter with a "factor" equal to 1 (or another arbitrary constant, therefore this factor is also called a constant). In this case, if you re-number the factors and parameters of the original model with this in mind (leaving the designation of the total number of factors - k), then the linear regression function can be written in the following form, which formally does not contain a constant:
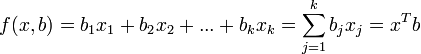
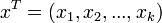 - vector of regressors,
- vector of regressors, 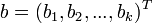 - column vector of parameters (coefficients)
- column vector of parameters (coefficients)
A linear model can be either with a constant or without a constant. Then, in this view, the first factor is either equal to one, or is the usual factor, respectively.
In the particular case when the factor is unique (without taking into account the constant), they speak of a pair or the simplest linear regression:
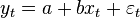
When the number of factors (without taking into account the constant) is greater than 1, then they say about multiple regression.
1. Organization cost model (without specifying a random error):
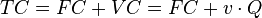
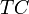 - total costs
- total costs 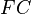 - fixed costs (not dependent on the volume of production),
- fixed costs (not dependent on the volume of production), 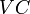 - variable costs proportional to the volume of production,
- variable costs proportional to the volume of production, 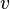 - specific or average (per unit of production) variable costs,
- specific or average (per unit of production) variable costs, 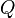 - volume of production.
- volume of production.
2. The simplest model of consumer spending (Keynes):
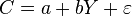
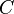 - consumer spending
- consumer spending 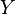 - disposable income
- disposable income 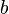 - “marginal propensity to consume”,
- “marginal propensity to consume”, 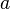 - Autonomous (not dependent on income) consumption.
- Autonomous (not dependent on income) consumption.
Let the sample be given a volume of n observations of the variables y and x . Let t be the number of observations in the sample. Then 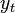 - the value of the variable y in the t -th observation,
- the value of the variable y in the t -th observation, 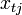 - the value of the j -th factor in the t -th observation. Respectively,
- the value of the j -th factor in the t -th observation. Respectively, 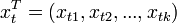 - vector of regressors in the t -th observation. Then a linear regression dependence occurs in each observation:
- vector of regressors in the t -th observation. Then a linear regression dependence occurs in each observation:
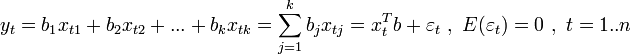
We introduce the notation:
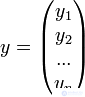 - vector of observations of the dependent variable y ,
- vector of observations of the dependent variable y , 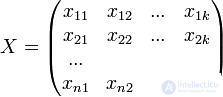 - matrix of factors.
- matrix of factors. 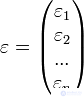 - vector of random errors.
- vector of random errors.
Then the linear regression model can be represented in a matrix form:
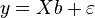
In classical linear regression, it is assumed that, along with the standard condition 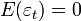 The following assumptions are also fulfilled ( Gauss-Markov conditions ):
The following assumptions are also fulfilled ( Gauss-Markov conditions ):
1) Homoscedasticity (constant or identical dispersion) or the absence of heteroscedasticity of random model errors: 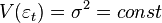
2) Absence of autocorrelation of random errors: 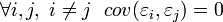
These assumptions in the matrix representation of the model are formulated as one assumption about the structure of the covariance matrix of the random error vector: 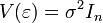
In addition to these assumptions, in the classical model, the factors are assumed to be deterministic ( non-stochastic ). In addition, it is formally required that the matrix 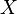 had a full rank (
had a full rank ( 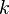 ), that is, it is assumed that there is no complete collinearity of factors.
), that is, it is assumed that there is no complete collinearity of factors.
When performing classical assumptions, the usual method of least squares allows one to obtain sufficiently qualitative estimates of the model parameters, namely: they are unbiased, consistent and most effective estimates.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis