Lecture
When investigating issues related to firing remote projectiles, one has to deal with the law of distribution of the points of rupture of a remote projectile in space. Subject to the use of conventional remote fuses, this distribution law can be considered normal.
In this 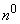 we consider only the canonical form of the normal law in space:
we consider only the canonical form of the normal law in space:
 , (9.6.1)
, (9.6.1)
Where 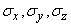 - main standard deviations.
- main standard deviations.
Moving from standard deviations to probable, we have:
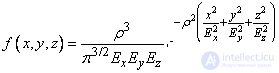 . (9.6.2)
. (9.6.2)
When solving problems associated with firing remote projectiles, it is sometimes necessary to calculate the probability of a remote projectile rupture within a given area. 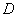 . In general, this probability is triggered by a triple integral:
. In general, this probability is triggered by a triple integral:
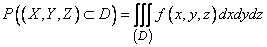 . (9.6.3)
. (9.6.3)
The integral (9.6.3) is usually not expressed in terms of elementary functions. However, there are a number of areas, the probability of falling into which is calculated relatively simply.
1. The probability of hitting a rectangular parallelepiped with sides parallel to the main dispersion axes
Let the area 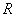 is a rectangular parallelepiped bounded by abscissas
is a rectangular parallelepiped bounded by abscissas  ordinates
ordinates  and appliques
and appliques 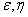 (fig. 9.6.1). Probability of hitting the area
(fig. 9.6.1). Probability of hitting the area 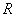 obviously equal to:
obviously equal to:
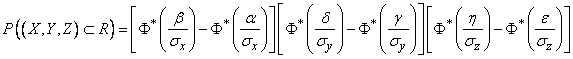 . (9.6.4)
. (9.6.4)
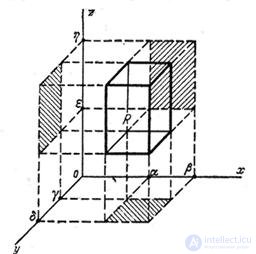
Fig. 9.6.1
2. The probability of hitting an ellipsoid of equal density
Consider an ellipsoid of equal density 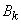 whose equation
whose equation
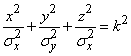 .
.
The semi-axes of this ellipsoid are proportional to the main standard quadratic deviations:
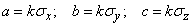 .
.
Using the formula (9.6.1) for 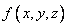 express the probability of hitting an ellipsoid
express the probability of hitting an ellipsoid 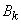 :
:
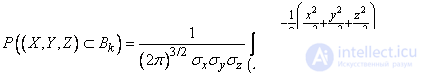 .
.
Let's move from Cartesian coordinates to polar (spherical) change of variables.
 (9.6.5)
(9.6.5)
The conversion Jacobian (9.6.5) is equal to:
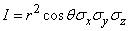 .
.
Turning to the new variables, we have:
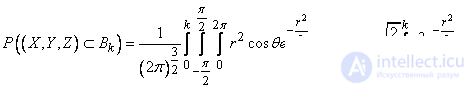 .
.
Integrating in parts, we get:
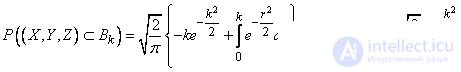 . (9.6.6)
. (9.6.6)
3. The probability of hitting a cylindrical region with a generator parallel to one of the main scattering axes
Consider a cylindrical shine 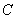 whose generator is parallel to one of the main dispersion axes (for example,
whose generator is parallel to one of the main dispersion axes (for example, 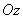 ), and the guide is the contour of an arbitrary area
), and the guide is the contour of an arbitrary area 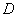 on surface
on surface 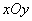 (fig. 9.6.2). Let the area
(fig. 9.6.2). Let the area 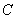 limited to two planes
limited to two planes 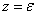 and
and 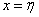 . Calculate the probability of hitting the area
. Calculate the probability of hitting the area 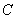 ; this is the probability of producing two events, the first of which consists in hitting a point
; this is the probability of producing two events, the first of which consists in hitting a point 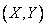 to the area
to the area 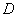 , and the second - in hit values
, and the second - in hit values 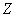 on the plot
on the plot  . As magnitudes
. As magnitudes 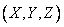 , subject to the normal law in canonical form, independent, then these two events are also independent. therefore
, subject to the normal law in canonical form, independent, then these two events are also independent. therefore
 (9.6.7)
(9.6.7)
Fig. 9.6.2.
Probability 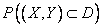 in formula (9.6.7) can be calculated by any of the methods for calculating the probability of hitting a flat region.
in formula (9.6.7) can be calculated by any of the methods for calculating the probability of hitting a flat region.
The following method for calculating the probability of hitting the spatial domain is based on the formula (9.6.7) 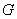 freeform: region
freeform: region 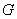 approximately divided into a number of cylindrical areas
approximately divided into a number of cylindrical areas 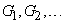 (fig. 9.6.3), and the probability of hitting each of them is calculated by the formula (9.6.7). To use this method, it is enough to draw a series of figures representing sections of the area
(fig. 9.6.3), and the probability of hitting each of them is calculated by the formula (9.6.7). To use this method, it is enough to draw a series of figures representing sections of the area 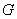 planes parallel to one of the coordinate planes. The probability of hitting each of them is calculated by the scattering grid.
planes parallel to one of the coordinate planes. The probability of hitting each of them is calculated by the scattering grid.
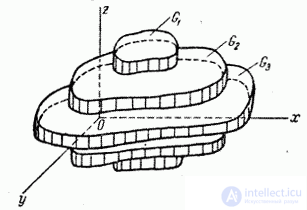
Fig. 9.6.3.
In conclusion of this chapter, we write the general for a normal law in the space of any number of dimensions 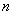 . The distribution density of such a law is:
. The distribution density of such a law is:
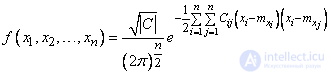 , (9.6.8)
, (9.6.8)
Where 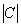 - determinant of the matrix
- determinant of the matrix 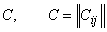 - inverse matrix of the correlation matrix
- inverse matrix of the correlation matrix 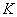 i.e. if correlation matrix
i.e. if correlation matrix
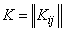 ,
,
that
 ,
,
Where 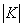 - the determinant of the correlation matrix, and
- the determinant of the correlation matrix, and 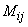 - the minor of this determinant, obtained from it by striking out
- the minor of this determinant, obtained from it by striking out 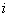 line and
line and 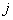 th column. notice, that
th column. notice, that
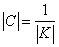 .
.
From the general expression (9.6.8) follow all forms of the normal law for any number of measurements and for any kinds of dependence between random variables. In particular, when  (dispersion in a plane) correlation matrix is
(dispersion in a plane) correlation matrix is
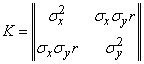 .
.
Where 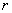 - correlation coefficient. From here
- correlation coefficient. From here
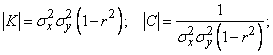
 .
.
Substituting the determinant of the matrix 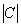 and its members in (9.6.8), we obtain the formula (9.1.1) for the normal law on the plane with which we started
and its members in (9.6.8), we obtain the formula (9.1.1) for the normal law on the plane with which we started 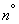 9.1.
9.1.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis