Lecture
Let there be a random variable 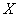 with mathematical expectation
with mathematical expectation 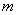 and variance
and variance 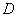 ; both parameters are unknown. Above magnitude
; both parameters are unknown. Above magnitude 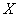 produced
produced 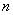 independent experiments that gave results
independent experiments that gave results 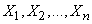 . It is required to find consistent and unbiased estimates for parameters
. It is required to find consistent and unbiased estimates for parameters 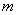 and
and 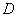 .
.
As an estimate for the mathematical expectation, it is natural to propose an arithmetic average of the observed values (previously we denoted it 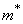 ):
):
 . (14.2.1)
. (14.2.1)
It is easy to verify that this estimate is consistent: according to the law of large numbers, with increasing 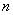 magnitude
magnitude 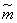 converges in probability to
converges in probability to 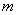 . Evaluation
. Evaluation 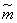 is also unbiased since
is also unbiased since
 . (14.2.2)
. (14.2.2)
The variance of this estimate is:
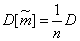 . (14.2.3)
. (14.2.3)
The effectiveness or inefficiency of the assessment depends on the type of distribution law 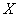 . It can be proved that if
. It can be proved that if 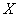 distributed according to the normal law, the variance (14.2.3) will be minimally possible, i.e.
distributed according to the normal law, the variance (14.2.3) will be minimally possible, i.e. 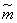 is effective. For other distribution laws this may not be the case.
is effective. For other distribution laws this may not be the case.
We proceed to estimate for variance. 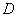 . At first glance, the statistical dispersion seems to be the most natural estimate:
. At first glance, the statistical dispersion seems to be the most natural estimate:
 , (14.2.4)
, (14.2.4)
Where
 . (14.2.5)
. (14.2.5)
Check if this estimate is consistent. Express it through the second initial moment (according to the formula (7.4.6) Chapter 7):
 . (14.2.6)
. (14.2.6)
The first term in the right side is the arithmetic mean 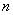 observed values of random variable
observed values of random variable 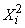 ; he converges in probability to
; he converges in probability to 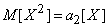 . The second term converges in probability to
. The second term converges in probability to 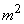 ; the entire quantity (14.2.6) converges in probability to the value
; the entire quantity (14.2.6) converges in probability to the value
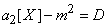 .
.
This means that the estimate (14.2.4) is consistent.
Check if the score is 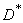 also unbiased. Substitute in the formula (14.2.6) instead of
also unbiased. Substitute in the formula (14.2.6) instead of 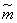 its expression (14.2.5) and perform the specified actions:
its expression (14.2.5) and perform the specified actions:


 . (14.2.7)
. (14.2.7)
Find the expected value (14.2.7):
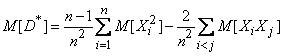 . (14.2.8)
. (14.2.8)
Since the variance 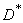 does not depend on which point you select the origin of coordinates, choose it at the point
does not depend on which point you select the origin of coordinates, choose it at the point 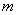 . Then
. Then
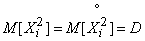 ;
; 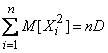 , (14.2.9)
, (14.2.9)
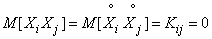 . (14.2.10)
. (14.2.10)
The last equality follows from the fact that the experiments are independent.
Substituting (14.2.9) and (14.2.10) into (14.2.8), we get:
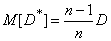 . (14.2.11)
. (14.2.11)
This shows that 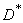 not an unbiased estimate for
not an unbiased estimate for 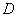 : her expectation is not equal
: her expectation is not equal 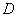 and somewhat less. Using the assessment
and somewhat less. Using the assessment 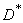 instead of dispersion
instead of dispersion 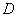 , we will make some systematic error down. To eliminate this bias, it is enough to introduce an amendment by multiplying the value
, we will make some systematic error down. To eliminate this bias, it is enough to introduce an amendment by multiplying the value 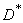 on
on 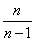 . We get:
. We get:
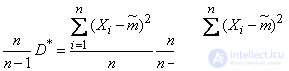 .
.
We will choose such a “corrected” statistical variance as an estimate for 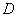 :
:
 . (14.2.12)
. (14.2.12)
Since the multiplier 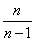 tends to unit when
tends to unit when 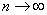 and score
and score 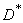 wealthy then estimate
wealthy then estimate 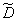 will also be wealthy.
will also be wealthy.
In practice, instead of formula (14.2.12), it is often more convenient to apply another, equivalent to it, in which the statistical dispersion is expressed through the second initial moment:
 . (14.2.13)
. (14.2.13)
For large values 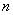 naturally both estimates are biased
naturally both estimates are biased 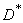 and unbiased
and unbiased 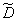 - there will be very little difference and the introduction of a correction factor loses its meaning.
- there will be very little difference and the introduction of a correction factor loses its meaning.
Thus, we have arrived at the following rules for processing limited statistical material.
If given values  taken in
taken in 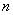 independent experiences random variable
independent experiences random variable 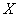 with unknown expectation
with unknown expectation 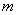 and variance
and variance 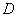 , then to determine these parameters should be used approximate values (estimates):
, then to determine these parameters should be used approximate values (estimates):
 (14.2.14)
(14.2.14)
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis