Lecture
Generating the moment function is a method of defining probability distributions. It is used most often for calculating moments.
Let there be a random variable 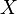 with distribution
with distribution 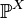 . Then its generating function of moments is called a function that has the form:
. Then its generating function of moments is called a function that has the form:
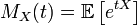 .
.
Using the formulas for calculating the expectation, the definition of the generating function of moments can be rewritten in the form:
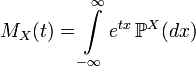 ,
,
that is, the generating function of moments is a two-sided Laplace transform of the distribution of a random variable (up to reflection).
If a random variable 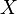 discrete, that is
discrete, that is 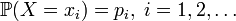 then
then
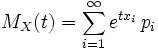 .
.
Example. Let be 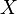 has a Bernoulli distribution. Then
has a Bernoulli distribution. Then
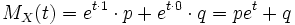 .
.
If a random variable 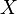 absolutely continuous, meaning it has a density
absolutely continuous, meaning it has a density 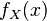 then
then
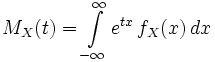 .
.
Example. Let be 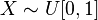 has a standard continuous uniform distribution. Then
has a standard continuous uniform distribution. Then
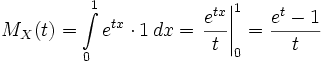 .
.
The properties of the generating functions of moments are in many respects similar to the properties of the characteristic functions due to the similarity of their definitions.
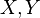 are two random variables, and
are two random variables, and 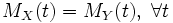 . Then
. Then 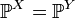 . In particular, if both quantities are absolutely continuous, then the coincidence of the generating functions of the moments implies the coincidence of the densities. If both random variables are discrete, then the coincidence of the generating functions of the moments implies the coincidence of the probability functions.
. In particular, if both quantities are absolutely continuous, then the coincidence of the generating functions of the moments implies the coincidence of the densities. If both random variables are discrete, then the coincidence of the generating functions of the moments implies the coincidence of the probability functions.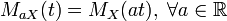 .
.
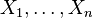 are independent random variables. Denote
are independent random variables. Denote 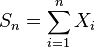 . Then
. Then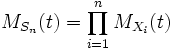 .
.
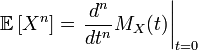 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis