Lecture
In the previous chapter, we familiarized ourselves with the methods for directly determining probabilities, namely, with the classical formula for the probability of an event, which reduces to a pattern of cases, and with a method of approximate determination of frequency probability for an event that does not boil down to a pattern of cases. However, not these immediate methods are fundamental in the theory of probability: their application is not always convenient and is not always possible. Even when an event is reduced to a pattern of cases, often this pattern is too complicated, and a direct calculation of the probability by the formula (2.2.1) becomes excessively cumbersome. As for the events that are not reducible to the scheme of cases, their probabilities are only rarely determined directly by frequencies. In practice, it is usually necessary to determine the probabilities of events whose direct experimental reproduction is difficult. For example, if you want to determine the probability of hitting an aircraft in air combat, it is clear that determining this probability by frequency is almost impossible. And not only because such experiments would turn out to be prohibitively complex and expensive, but also because we often need to estimate the probability of a particular outcome of the battle not for the existing types of equipment, but for promising, designed ones. Usually, such an assessment is made in order to identify the most rational design parameters of the elements of promising technology.
Therefore, as a rule, not direct methods are used to determine the probabilities of events, but indirect ones, which allow determining the probabilities of other events related to them by the known probabilities of some events. The whole theory of probability, basically, is a system of such indirect methods, the use of which allows to reduce the necessary experiment to a minimum.
Using these indirect methods, we always use the basic theorems of probability theory in one form or another. There are two theorems: the probability addition theorem and the probability multiplication theorem. Strictly speaking, both of these statements are theorems and can only be proved for events that reduce to the scheme of cases. For events that are not reducible to the scheme of cases, they are accepted axiomatically, as principles or postulates.
Before formulating and proving the main theorems, we introduce some auxiliary concepts, namely, the concepts of the sum of events and the product of events.
In many areas of the exact sciences, symbolic operations are used on various objects, which receive their names by analogy with arithmetic operations, a number of properties of which they possess. Such, for example, are the operations of addition and multiplication of vectors in mechanics, the operations of addition and multiplication of matrices in algebra, etc. These operations, subject to well-known rules, allow not only to simplify the form of records, but in some cases greatly facilitate the logical construction of scientific conclusions. The introduction of such symbolic operations on events is fruitful in the theory of probability.
The sum of two events 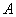 and
and 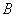 called event
called event 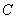 event execution
event execution 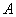 or events
or events 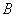 or both together.
or both together.
For example, if an event 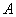 - hitting the target at the first shot, event
- hitting the target at the first shot, event 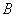 - hitting the target with the second shot, the event
- hitting the target with the second shot, the event 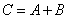 there is a hit in general, it does not matter at what shot - at the first, at the second, or at both together.
there is a hit in general, it does not matter at what shot - at the first, at the second, or at both together.
If events 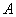 and
and 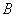 incompatible, it is natural that the occurrence of these events together disappears, and the sum of the events
incompatible, it is natural that the occurrence of these events together disappears, and the sum of the events 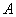 and
and 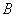 comes down to an appearance or event
comes down to an appearance or event 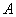 or events
or events 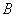 . For example, if an event
. For example, if an event 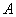 - the appearance of the card of the suit color when removing the card from the deck, the event
- the appearance of the card of the suit color when removing the card from the deck, the event 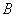 - the appearance of the card of the diamonds suit, then
- the appearance of the card of the diamonds suit, then 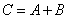 there is the appearance of a card of the red suit, no matter - a red or diamonds.
there is the appearance of a card of the red suit, no matter - a red or diamonds.
In short, the sum of two events 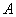 and
and 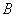 called event
called event 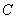 consisting of the appearance of at least one of the events
consisting of the appearance of at least one of the events 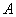 and
and 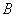 .
.
The sum of several events is an event consisting of the appearance of at least one of these events.
For example, if the experience consists of five shots on the target and the events are given:
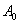 - not a single hit,
- not a single hit,
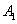 - exactly one hit,
- exactly one hit,
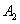 - exactly two hits,
- exactly two hits,
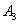 - exactly three hits,
- exactly three hits,
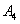 - exactly four hits,
- exactly four hits,
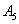 - exactly five hits,
- exactly five hits,
that
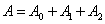
there is an event "no more than two hits", and
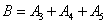
There is an event "at least three hits."
The product of two events 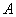 and
and 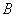 called event
called event 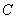 consisting in the joint execution of the event
consisting in the joint execution of the event 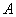 and events
and events 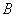 .
.
For example, if an event 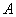 - the appearance of an ace when drawing a card from the deck, an event
- the appearance of an ace when drawing a card from the deck, an event 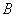 - the appearance of the card of the diamonds suit, the event
- the appearance of the card of the diamonds suit, the event 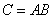 there is the appearance of a diamond ace. If you make two shots at the target and the event
there is the appearance of a diamond ace. If you make two shots at the target and the event 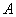 - hit at the first shot, event
- hit at the first shot, event 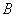 - hit with the second shot, then
- hit with the second shot, then 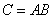 There is a hit with both shots.
There is a hit with both shots.
The product of several events is an event consisting in the co-occurrence of all these events.
For example, if three shots are fired at a target and events are considered
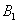 - miss at the first shot,
- miss at the first shot,
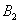 - miss in the second shot,
- miss in the second shot,
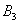 - slip at the third shot,
- slip at the third shot,
that event
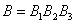
consists in the fact that the target will not be a single hit.
In determining probabilities, it is often necessary to represent complex events as combinations of simpler events, using both the addition operation and the event multiplication operation.
For example, let the target make three shots and consider the following elementary events:
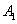 - hit at the first shot,
- hit at the first shot,
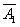 - miss at the first shot,
- miss at the first shot,
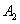 - hit with the second shot,
- hit with the second shot,
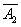 - miss in the second shot,
- miss in the second shot,
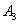 - hit with the third shot,
- hit with the third shot,
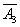 - miss in the third shot.
- miss in the third shot.
Consider a more complex event. 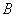 , consisting in the fact that as a result of these three shots will be exactly one hit in the target. Event
, consisting in the fact that as a result of these three shots will be exactly one hit in the target. Event 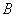 can be represented as the following combination of elementary events:
can be represented as the following combination of elementary events:
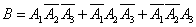 .
.
Event 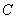 , consisting in the fact that the target will be at least two hits, can be represented as:
, consisting in the fact that the target will be at least two hits, can be represented as:
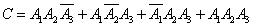 .
.
Such techniques for presenting complex events are often used in probability theory.
Directly from the definition of the sum and the product of events it follows that
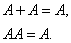
If an event 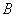 there is a special case of the event
there is a special case of the event 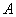 then
then
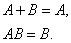
When using the concepts of the sum and product of events, it is often helpful to have a visual geometric interpretation of these concepts.
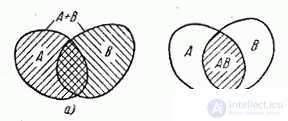
Fig. 3.1.1.
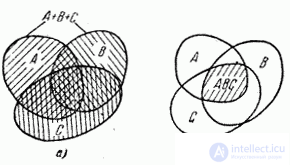
Fig. 3.1.2.
In fig. 3.1.1 the concepts of the sum and product of two events are clearly illustrated. If an event 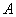 there is a point in the region
there is a point in the region 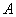 respectively event
respectively event 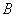 - hit the area
- hit the area 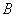 then event
then event 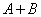 there is a hit in the area shaded in fig. 3.1.1, a), and the event
there is a hit in the area shaded in fig. 3.1.1, a), and the event 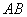 - to the area shaded in fig. 3.1.1, b). In fig. 3.1.2 similarly shows the sum and product of the three events.
- to the area shaded in fig. 3.1.1, b). In fig. 3.1.2 similarly shows the sum and product of the three events.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis