Lecture
Generating function (or generator ) sequence 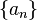 - this is a formal power series
- this is a formal power series
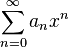 .
.
Often, the generating function of a sequence of numbers is the Taylor series of some analytic function, which can be used to study the properties of the sequence itself. However, in the general case, the generating function does not have to be analytic. For example, both rows
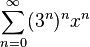 and
and 
have a radius of convergence of zero, that is, diverge at all points except zero, and at zero both are equal to 1, that is, as functions, they coincide; nevertheless, they differ as formal ranks.
The generating functions make it possible to simply describe many complex sequences in combinatorics, and sometimes help to find explicit formulas for them.
The method of generating functions was developed by Euler in the 1750s.
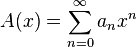 and
and 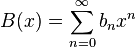 sequences
sequences 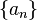 and
and 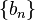 is a convolution generating function
is a convolution generating function 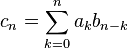 these sequences:
these sequences: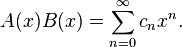
Let be 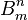 Is the number of compositions of a non-negative integer n of length m , that is, representations of n in the form
Is the number of compositions of a non-negative integer n of length m , that is, representations of n in the form 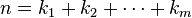 where
where 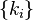 - non-negative integers. Number
- non-negative integers. Number 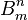 It is also the number of combinations with repetitions of m through n , that is, the number of samples n possibly repeating elements from the set
It is also the number of combinations with repetitions of m through n , that is, the number of samples n possibly repeating elements from the set 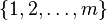 (with each member
(with each member 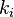 in the composition can be interpreted as the number of elements i in the sample).
in the composition can be interpreted as the number of elements i in the sample).
For a fixed m generating function of the sequence 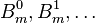 is an:
is an:
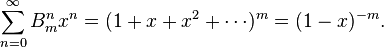
Therefore number 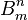 can be found as a coefficient for
can be found as a coefficient for 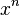 in decomposition
in decomposition 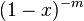 by powers of x . To do this, you can use the definition of the binomial coefficients, or directly take the derivative n times at zero:
by powers of x . To do this, you can use the definition of the binomial coefficients, or directly take the derivative n times at zero:
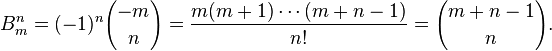
 - positive integer random variable (special case discrete), having a probability distribution
- positive integer random variable (special case discrete), having a probability distribution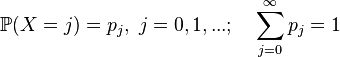
then its expectation can be expressed in terms of the generating function of the sequence 
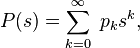
as the value of the first derivative in the unit: 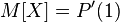 (It is worth noting that the series for P (s) converges, at least when
(It is worth noting that the series for P (s) converges, at least when 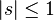 ). Really,
). Really,
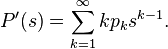
When substitution 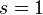 get the value
get the value 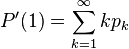 , which by definition is the expectation of a discrete random variable. If this series diverges, then
, which by definition is the expectation of a discrete random variable. If this series diverges, then 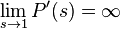 -- but
-- but  has infinite mathematical expectation
has infinite mathematical expectation 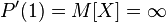
 sequences of tails of distribution
sequences of tails of distribution 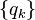
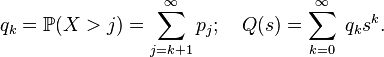
This generating function is associated with a previously defined function.  property:
property: 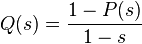 at
at 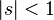 . From this, by the mean-theorem, it follows that the expectation is equal to just the value of this function in the unit:
. From this, by the mean-theorem, it follows that the expectation is equal to just the value of this function in the unit:
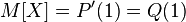
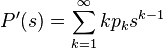 and using the ratio
and using the ratio 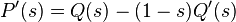 , we get:
, we get: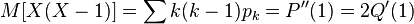
To get the variance 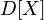 , this expression must be added
, this expression must be added 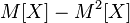 , which leads to the following formulas for calculating the variance:
, which leads to the following formulas for calculating the variance:
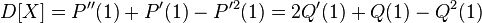 .
.
In case of infinite dispersion 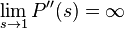 .
.
Exponential generating function of a sequence 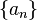 - this is a formal power series
- this is a formal power series
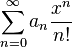 .
.
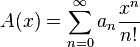 and
and 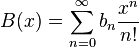 - exponential generating functions of sequences
- exponential generating functions of sequences 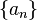 and
and 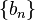 then their work
then their work 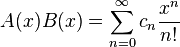 is an exponential generating function of a sequence
is an exponential generating function of a sequence 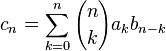 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis