Lecture
In the combo of the general generation (synonim - living functions [1], in English - the generating function , the Russian is the generating function ) 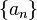 - full formal degree series
- full formal degree series
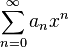 .
.
Exponential generatrix (two functions) - a formal degree series
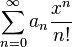 .
.
Dovolі often generatrix (two functions) sequential 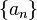 One hour next to Taylor's vidomoj analogy functions, the Vikorisovuvati center at the complete power of self-sufficiency. Tim is not less, generations are not necessarily dependent on the analog functions.
One hour next to Taylor's vidomoj analogy functions, the Vikorisovuvati center at the complete power of self-sufficiency. Tim is not less, generations are not necessarily dependent on the analog functions.
Napriklad, two rows
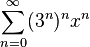 і
і 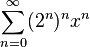
May radius zbіzhnosti zero, tobto rozbіgayutsya at usih points, crіm zero, and at zero offended give 1, tobto yak funktsіya stinks zbіgayutsya; Tim not less, yak generaltrisi (tobto formal rows) stink rіznі.
The generatrices (functions) give the opportunity to simply describe the folding of the sequence, and others want to know the obvious formulas for them. The method of generation of Euler in the 50s of the 18th century.
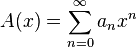 і
і 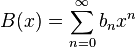 —Generacy successions
—Generacy successions 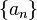 і
і 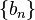 then
then 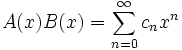 de
de 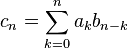 .
.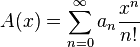 і
і 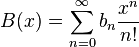 - ekspononentsіynі generatrix of successions
- ekspononentsіynі generatrix of successions 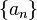 і
і 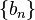 then
then 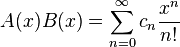 de
de 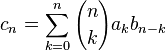 .
.Nehaj  Dear Kilkost Variant presented number
Dear Kilkost Variant presented number  viglyadі
viglyadі 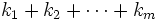 where
where 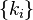 - nevid'nm number of numbers і
- nevid'nm number of numbers і 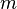 fiksovano, Todi
fiksovano, Todi
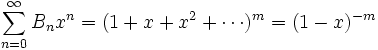
Now number 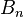 you can know yak kodіfііnt
you can know yak kodіfііnt 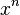 in rozklad_
in rozklad_ 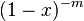 by degrees
by degrees 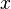 . For tsogo, you can skachatitsya znachitelnyam bіnomіalnyh koyfіtsієntvv abo Well without a second take n raziv pokіdnu to zero:
. For tsogo, you can skachatitsya znachitelnyam bіnomіalnyh koyfіtsієntvv abo Well without a second take n raziv pokіdnu to zero:
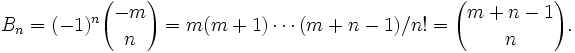
Do not shift the term " generating function " from the English not to reach it far away. Crash Vikorisovuvati natom_st bіlsh implantations termіn in Ukrainian Mathematical Literature - " tvirna funktsiya ", Yakomi vіdpovіdaє Rosіyske " producing function " [2].
In mathematics, two powerful directions can be distinguished: one studies continuous objects, the other discrete ones. In the real world there is a place for that and for a different approach and it is often possible to approach the study of the same phenomenon from different points of view. Of course, between these areas there are many connections. The article is devoted to one of them. The idea of the generating function is very simple. We compare the sequences a0, a1, ..., an, ... (to a discrete object) by the power series a0 + a1x + ... + anxn + ... (a continuous object). Doing this, we connect a powerful arsenal of tools for mathematical analysis to the study of discrete objects. Note that in the examples considered below, power series converge on a certain neighborhood of zero, although there is a theory of formal power series, which also considers power series that converge only at point 0. The uniqueness theorem is valid: if for some positive “c” the function f ( x) is representable as a power series a0 + + a1x + ... + anxn + ... on the interval (−c, s), then the coefficients ai of the series are uniquely determined. There are other constructions of generating functions - one of them is touched at the end of the article. We will use the properties of power series known from the basic course of mathematical analysis without additional instructions. Some properties and applications of power series are given in [1]. The method of generating functions is very productive, in particular when solving combinatorial problems. Let us give some initial examples. 1. The most famous example of a generating function is, of course, Newton's bin
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis