7.1. The main tasks of mathematical statistics

The mathematical laws of the theory of probability are not pointless abstractions, devoid of physical content; they are a mathematical expression of real laws that actually exist in mass random phenomena of nature.

So far, speaking of the laws of distribution of random variables, we have not touched on the question of where they come from, on what basis these laws of distribution are established. The answer to the question is quite definite - experience is the basis of all these characteristics; Each study of random phenomena performed by the methods of probability theory, directly or indirectly, is based on experimental data. Using such concepts as events and their probabilities, random variables, their distribution laws and numerical characteristics, probability theory makes it possible theoretically to determine the probabilities of some events through the probabilities of others, the laws of distribution and the numerical characteristics of some random variables through the laws of distribution and numerical characteristics of others. Such indirect methods can significantly save time and money spent on the experiment, but does not exclude the experiment itself. Each study in the field of random phenomena, however abstract it may be, is always rooted in experiment, in experimental data, in the observing system.

The development of methods for recording, describing and analyzing statistical experimental data obtained as a result of observing mass random phenomena is the subject of a special science — mathematical statistics.

All problems of mathematical statistics relate to the processing of observations of mass random phenomena, but depending on the nature of the practical problem being solved and on the amount of available experimental material, these tasks may take one form or another.

Let us briefly describe some typical problems of mathematical statistics that are often encountered in practice.

1. The task of determining the law of distribution of a random variable (or a system of random variables) according to statistical data

We have already indicated that the patterns observed in mass random phenomena are manifested the more precisely and clearly, the greater the volume of statistical material. When processing statistical data of extensive scope, the question of determining the laws of distribution of various random variables often arises. Theoretically, with a sufficient number of experiments, the patterns characteristic of these random variables will be carried out arbitrarily accurately. In practice, we always have to deal with a limited amount of experimental data; therefore, the results of our observations and their processing always contain a greater or lesser element of randomness. The question arises as to which features of the observed phenomenon are permanent, stable and inherent in it, and which are random and manifest themselves in this series of observations only due to the limited amount of experimental data. Naturally, such requirements should be made to the method of processing experimental data so that, if possible, it retains the typical, characteristic features of the observed phenomenon and discards everything insignificant, secondary, associated with an insufficient amount of experimental material. In this connection, the problem of smoothing or leveling statistical data, characteristic of mathematical statistics, and presenting them in the most compact form with the help of simple analytical dependencies arises.

2. The task of testing the likelihood of hypotheses

This task is closely related to the previous one; When solving such problems, we usually do not have such extensive statistical material that the statistical patterns that emerge in it are sufficiently free from the elements of randomness. Statistical material may with greater or lesser likelihood confirm or not confirm the validity of a particular hypothesis. For example, the following question may arise: are the experimental results consistent with the hypothesis that this random variable is subject to the distribution law 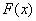? Another similar question: does the tendency observed in experience indicate a relationship between two random variables to the presence of a real objective relationship between them, or is it due to random reasons related to an insufficient amount of observations? To solve such questions, mathematical statistics has developed a number of special techniques.

3. The problem of finding the unknown distribution parameters

Often, when processing statistical material, there is no question at all about determining the distribution laws of the random variables under study. This is usually due to the extremely insufficient amount of experimental material. Sometimes the nature of the law of distribution is qualitatively known prior to experience, from theoretical considerations; for example, it can often be argued in advance that a random variable is subject to normal law. Then there is a narrower task of processing observations - to determine only some parameters (numerical characteristics) of a random variable or a system of random variables. With a small number of experiments, the problem of more or less accurate determination of these parameters can not be solved; in these cases, the experimental material contains inevitably a significant element of chance; therefore, all parameters calculated on the basis of this data are also random. In such conditions, only the task of determining the so-called “estimates” or “suitable values” for the desired parameters, that is, can be posed. such approximate values, which in the case of mass use, would on average lead to smaller errors than any others. The task of finding “suitable values” of numerical characteristics is closely related to the task of assessing their accuracy and reliability. We will meet with similar tasks in chapter 14.

This is not a complete list of the main tasks of mathematical statistics. We have listed only those of them that are most important to us in their practical applications. In this chapter, we will briefly introduce some of the most elementary problems of mathematical statistics and methods for solving them.