Lecture
Let the random variable 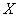 subject to normal law with density:
subject to normal law with density:
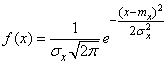 , (12.2.1)
, (12.2.1)
a random variable 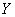 associated with her linear functional dependence:
associated with her linear functional dependence:
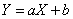 . (12.2.2)
. (12.2.2)
Where 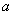 and
and 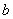 - non-random coefficients.
- non-random coefficients.
It is required to find the distribution law 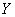 .
.
Let's issue a solution in the form of two columns, similar to the example of the previous one. 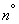 :
:
|
|
|
|
|
|
|
|
|
|
|
|
Transforming expression 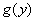 , we have:
, we have:
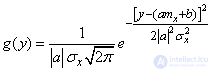 ,
,
and this is nothing but a normal law with parameters:
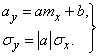 (12.2.3)
(12.2.3)
If we go from standard deviations to proportional probable deviations, we get:
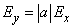 . (12.2.4)
. (12.2.4)
Thus, we have seen that the linear function of the argument subject to the normal law is also subject to the normal law. To find the center of dispersion of this law, it is necessary to substitute its center of dispersion in the expression of a linear function instead of the argument. To find the standard deviation of this law, you need to multiply the standard deviation of the argument by the modulus of the coefficient for the argument in the expression of a linear function. The same rule holds true for probable deviations.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis