Lecture
Probability function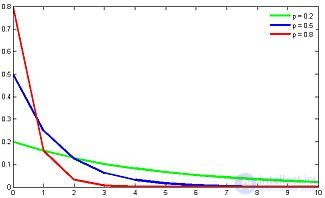 |
||
Distribution function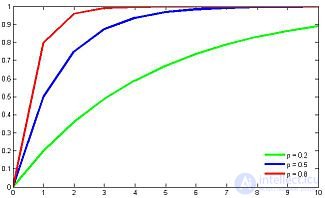 |
||
| Designation | 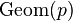 |
|
| Options |  —Number of “failures” before the first “success” —Number of “failures” before the first “success”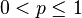 - the probability of "success" - the probability of "success"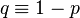 - probability of “failure” - probability of “failure” |
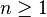 —Number of the first “success” —Number of the first “success”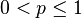 - the probability of "success" - the probability of "success"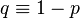 - probability of “failure” - probability of “failure” |
| Carrier | 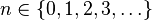 |
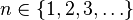 |
| Probability function | 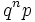 |
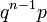 |
| Distribution function | 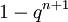 |
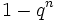 |
| Expected value | 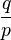 |
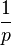 |
| Median | N / A | N / A |
| Fashion | 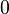 |
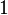 |
| Dispersion | 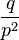 |
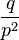 |
| Asymmetry coefficient | 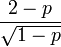 |
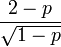 |
| Coefficient of kurtosis | 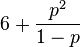 |
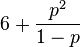 |
| Informational entropy | 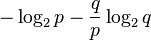 |
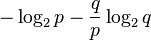 |
| Generating function of moments | 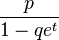 |
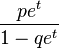 |
| Characteristic function | 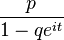 |
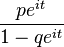 |
Geometric distribution in probability theory is the distribution of a discrete random value equal to the number of trials of a random experiment prior to the observation of the first “success”.
Let be 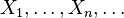 - an infinite sequence of independent random variables with the distribution of Bernoulli, that is,
- an infinite sequence of independent random variables with the distribution of Bernoulli, that is,
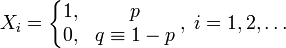
Construct a random variable 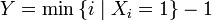 - the number of “failures” to the first “success”. Random distribution
- the number of “failures” to the first “success”. Random distribution 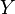 called geometric with probability of "success"
called geometric with probability of "success" 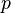 what is denoted as follows:
what is denoted as follows:  .
.
Probability function of a random variable 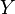 has the form:
has the form:
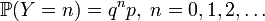
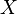 - the number of the first "success". Then the probability function takes the form
- the number of the first "success". Then the probability function takes the form 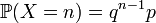 . The table on the right shows the formulas for both options.
. The table on the right shows the formulas for both options.The generating moment function of the geometric distribution has the form:
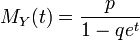 ,
,
from where
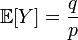 ,
,
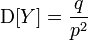 .
.
 and fixed average
and fixed average 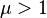 geometric distribution
geometric distribution 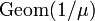 is one of the distributions with maximum informational entropy.
is one of the distributions with maximum informational entropy.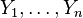 independent and
independent and 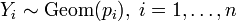 then
then .
.
If a  then
then 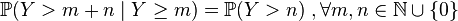 , that is, the number of past “failures” does not affect the number of future “failures”.
, that is, the number of past “failures” does not affect the number of future “failures”.
Geometric distribution is the only discrete distribution with the lack of memory property.
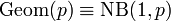 .
.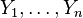 independent and
independent and 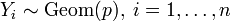 then
then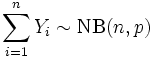 .
.
Let the dice roll before the first six falls out. Then the probability that we will need no more than three shots is equal to
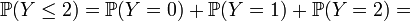
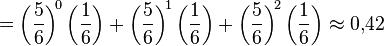 .
.
The expected number of shots is
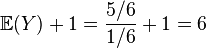 .
.
The geometric distribution law takes place in such sciences as microbiology, genetics, physics. In practice, the experiment or experience is carried out before the first occurrence of a successful event A. The number of attempts made will be an integer random variable 1,2, .... The probability of occurrence of event A in each experiment does not depend on the previous ones and is p, q = 1-p. The probabilities of possible values of a random variable X are determined by the dependence
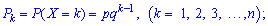
There is in all previous experiments except for the k-th the experiment gave a bad result and only in the k-th was it successful. This probability formula is called the geometric distribution law, since its right-hand side coincides with the expression of a common element of a geometric progression.
In tabular form, the geometric law of distribution is

When checking the normalization condition, we use the formula of the sum of an infinite geometric progression
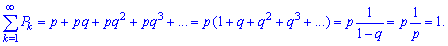
The probabilistic generating function is expressed by the formula
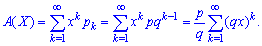
Insofar as  then the generating function can be summed
then the generating function can be summed
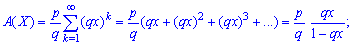
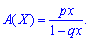
Numerical characteristics for the geometric law of probability distribution is determined by the formulas:
1. Mathematical expectation
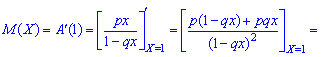
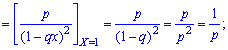
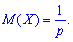
2. Dispersion and standard deviation by the formulas
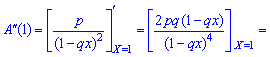
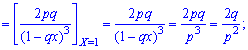
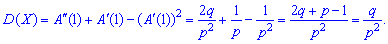
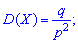
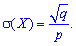
3. The coefficient of asymmetry and kurtosis for the geometric distribution is determined by the formula
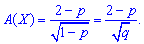
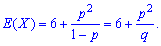
Among discrete random variables, only the geometric law is given the property of the absence of aftereffect. This means that the probability of occurrence of a random event in the k-th experiment does not depend on how many of them appeared before the k-th, and is always equal to p.
--------------------------------------
Example 1. A die is thrown before the first appearance of the number 1. Determine all the numerical characteristics of M (X), D (X), S (X), A (X), E (X) for a random variable X of the number of flips to be performed.
Decision. By the condition of the problem, the random variable X is integral with the geometric law of probability distribution. The probability of a successful flip is a constant and equal to one divided by the number of faces of the cube.
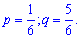
Having p, q necessary numerical characteristics of X we find the above formulas
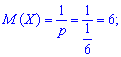
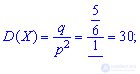
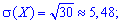
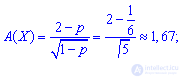
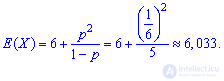
------------------------------------
Example 2. Amateur hunter shoots a gun at a fixed target. The probability of hitting the target with one shot is constant and equal to 0.65. Shooting at the target is before the first hit.
Determine the numerical characteristics M (X), D (X), S (X), A (X), E (X) of the number of cartridges spent by the hunter.
Decision. The random variable X obeys the geometric distribution law, therefore the probability of hitting in each attempt is constant and is p = 0.65; q = 1-p = 0.35.
By the formulas we calculate the expectation
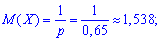
dispersion
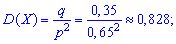
standard deviation
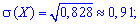
asymmetry
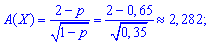
excess
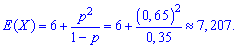
The calculation of numerical characteristics for the geometric distribution law is not so complicated, so use the formulas given in such problems and get only the correct results.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis