Lecture
There is a system 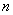 random variables:
random variables:
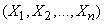
and set the numerical characteristics of the system: mathematical expectations
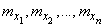
and correlation matrix
 .
.
Random value 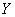 there is a function of arguments
there is a function of arguments 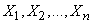 :
:
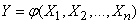 , (11.3.1)
, (11.3.1)
and function  not linear, but differs little from linear in the area of practically possible values of all arguments (in short, “almost linear” function). It is required to approximately find the numerical characteristics of the value
not linear, but differs little from linear in the area of practically possible values of all arguments (in short, “almost linear” function). It is required to approximately find the numerical characteristics of the value  - expected value
- expected value 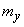 and variance
and variance 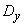 .
.
To solve the problem, we expose the linearization function
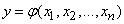 . (11.3.2)
. (11.3.2)
In this case, it makes no sense to use a geometric interpretation, since outside of the three-dimensional space, it no longer has the advantages of clarity. However, the qualitative side of the question remains exactly the same as in the previous  .
.
Consider the function 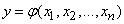 in a fairly small neighborhood of a point
in a fairly small neighborhood of a point 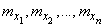 . Since the function in this neighborhood is almost linear, it can be approximately replaced by a linear one. This is equivalent to, in expanding a function in a Taylor series near a point
. Since the function in this neighborhood is almost linear, it can be approximately replaced by a linear one. This is equivalent to, in expanding a function in a Taylor series near a point 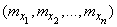 keep only the members of the first order, and all the higher ones reject:
keep only the members of the first order, and all the higher ones reject:
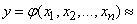
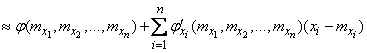 .
.
Hence, the dependence (11.3.1) between random variables can be approximately replaced by a linear dependence:
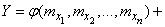
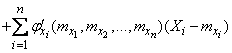 . (11.3.3)
. (11.3.3)
For brevity we introduce the notation:
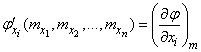 .
.
Considering that 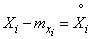 rewrite the formula (11.3.3) in the form:
rewrite the formula (11.3.3) in the form:
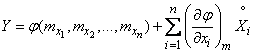 (11.3.4)
(11.3.4)
For the linear function (11.3.4), we apply the methods for determining the numerical characteristics of linear functions derived in  10.2. Keeping in mind that centered arguments
10.2. Keeping in mind that centered arguments  have a mathematical expectation of zero, and the same correlation matrix
have a mathematical expectation of zero, and the same correlation matrix 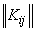 , we get:
, we get:
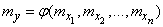 , (11.3.5)
, (11.3.5)
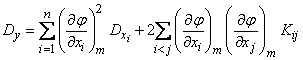 (11.3.6)
(11.3.6)
Passing in the last formula from dispersions to standard deviations, we get:
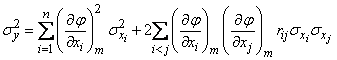 , (11.3.7)
, (11.3.7)
Where 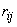 - coefficient of correlation of quantities
- coefficient of correlation of quantities 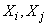 .
.
The formula (11.3.7) takes on a particularly simple form, when the quantities 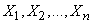 not correlated, i.e.
not correlated, i.e. 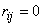 at
at 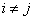 .
.
In this case
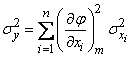 .
.
Formulas of the type (11.3.7) and (11.3.8) are widely used in various applied issues: in the study of errors of various types of devices and mechanisms, as well as in the analysis of accuracy of shooting and bombing.
Example 1. Bomb attribution  (fig. 11.3.1) is expressed by the approximate analytical formula:
(fig. 11.3.1) is expressed by the approximate analytical formula:
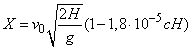 , (11.3.9)
, (11.3.9)
Where 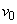 - aircraft speed (m / s),
- aircraft speed (m / s), 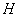 - drop height (m),
- drop height (m), 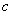 - ballistic coefficient.
- ballistic coefficient.

Fig. 11.3.1
Height 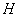 determined by altimeter, the speed of the aircraft
determined by altimeter, the speed of the aircraft 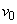 - according to speed indicator, ballistic coefficient
- according to speed indicator, ballistic coefficient 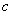 accepted by its nominal value
accepted by its nominal value 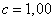 . Altimeter shows 4000 m, speed indicator 150 m / s. The altimeter readings are characterized by a systematic error of +50 m and standard deviation
. Altimeter shows 4000 m, speed indicator 150 m / s. The altimeter readings are characterized by a systematic error of +50 m and standard deviation 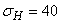 m; readings of the speed indicator - by systematic error - 2 m / s and standard deviation of 1 m / s; scatter of the possible values of the ballistic coefficient
m; readings of the speed indicator - by systematic error - 2 m / s and standard deviation of 1 m / s; scatter of the possible values of the ballistic coefficient 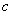 due to the inaccuracy of the manufacture of the bomb, characterized by a standard deviation
due to the inaccuracy of the manufacture of the bomb, characterized by a standard deviation 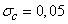 . Instrument errors are independent of each other.
. Instrument errors are independent of each other.
Find the systematic error and the standard deviation of the point of incidence of the bomb due to inaccuracy in determining the parameters 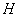 ,
, 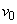 and
and 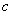 . Determine which of these factors has the greatest influence on the scatter of the point of the bomb falling.
. Determine which of these factors has the greatest influence on the scatter of the point of the bomb falling.
Decision. Values 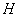 ,
, 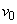 and
and 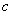 are uncorrelated random variables with numerical characteristics:
are uncorrelated random variables with numerical characteristics:
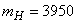 m;
m; 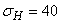 m;
m;
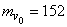 m / s;
m / s; 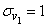 m / s;
m / s;
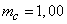 ;
; 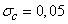 .
.
Since the range of possible changes in random arguments is relatively small, the linearization method can be used to solve the problem.
Substituting in the formula (11.3.9) instead of the values 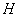 ,
, 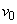 and
and 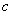 their mathematical expectations, we will find the mathematical expectation of the value
their mathematical expectations, we will find the mathematical expectation of the value 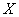 :
:
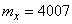 (m)
(m)
For comparison, we calculate the nominal value:
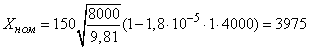 (m)
(m)
The difference between the expectation and the nominal value is the systematic error of the drop point:
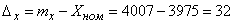 (m)
(m)
To determine the variance of 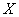 calculate the partial derivatives:
calculate the partial derivatives:
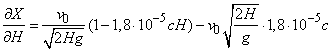 ,
,
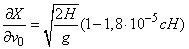 ,
,
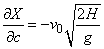
and substitute in these expressions for each argument its expectation:
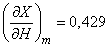 ;
; 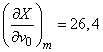 ;
; 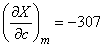 .
.
By the formula (11.3.8) we calculate the standard deviation of 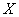 :
:
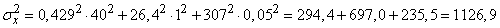 ,
,
from where
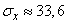 (m)
(m)
Comparing the terms forming  , we conclude that the largest of them (697.0) is due to the presence of errors in speed
, we conclude that the largest of them (697.0) is due to the presence of errors in speed 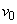 ; therefore, under the given conditions, of the considered random factors responsible for the scatter of the point of bomb fall, the speed indicator error is the most significant.
; therefore, under the given conditions, of the considered random factors responsible for the scatter of the point of bomb fall, the speed indicator error is the most significant.
Example 2. The abscissa of the hit point (in meters) when shooting at an airplane is expressed by the formula
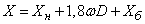 , (11.3.10)
, (11.3.10)
Where 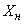 - error pickup (m)
- error pickup (m) 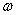 - angular velocity of the target (rad / sec),
- angular velocity of the target (rad / sec), 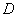 - firing range (m),
- firing range (m), 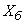 - error related to projectile ballistics (m).
- error related to projectile ballistics (m).
Values 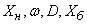 are random variables with mathematical expectations:
are random variables with mathematical expectations:
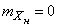 ;
; 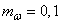 ;
; 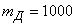 ;
; 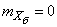
and mean square deviations:
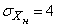 ;
; 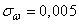 ;
; 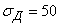 ;
; 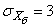 .
.
The normalized correlation matrix of the system ( 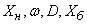 ) (i.e. the matrix composed of the correlation coefficients) has the form:
) (i.e. the matrix composed of the correlation coefficients) has the form:
 .
.
It is required to find the mathematical expectation and standard deviation of 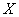 .
.
Decision. Substituting into the formula (11.3.10) the mathematical expectations of the arguments, we have:
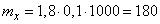 (m)
(m)
To determine the standard deviation of 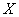 find partial derivatives:
find partial derivatives:
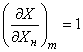 ;
; 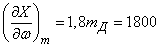 ;
;
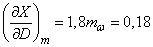 ;
; 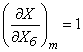 .
.
Applying the formula (11.3.7), we have:
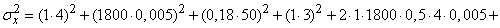
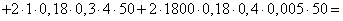
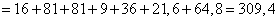 ,
,
from where
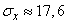 (m)
(m)
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis