49. The relative position of a point, a line and a plane.

A straight line may or may not belong to a plane. It belongs to a plane if at least two points of it lie on a plane. In fig. 93 shows the Sum (axb) plane . Line l belongs to the Sum plane, since its points 1 and 2 belong to this plane.

If the line does not belong to a plane, it can be parallel to it or intersect it.

A straight line is parallel to the plane, if it is parallel to another straight line.

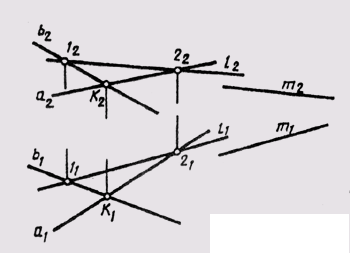
Fig. 93

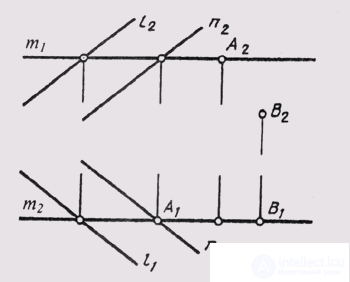
Fig. 94

my lying in that plane. In fig. 93 straight m || Sum , since it is parallel to the line l belonging to this plane.

A straight line can intersect a plane at different angles and, in particular, be perpendicular to it. The construction of the lines of intersection of the line with the plane is given in §61.

A point in relation to a plane can be located as follows: to belong or not to belong to it. A point belongs to a plane if it is located on a straight line located in this plane. In fig. 94 shows a complex drawing of the Sum plane defined by two parallel straight lines l and n. The plane m is located in the plane . Point A lies in the Sum plane, since it lies on the line m. Point B does not belong to the plane, since its second projection does not lie on the corresponding projections of the line.