22. Local curves

Lekalnye called flat curves, drawn with the help of patterns on previously constructed points. By lekalnyh curves include: ellipse parabola, hyperbola, cycloid, sinewave involute, etc.

An ellipse is a second-order closed flat curve. It is characterized by the fact that the sum of the distances from any of its

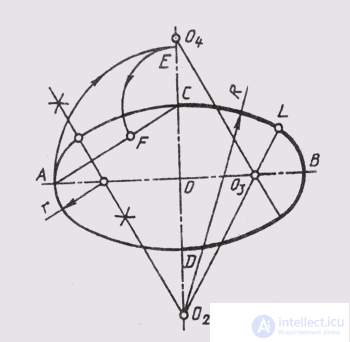
Fig. 36

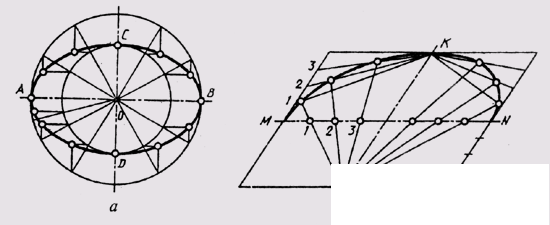
Fig. 37

points to two points of foci is a constant value equal to the larger axis of the ellipse. You can build an ellipse in several ways. For example, you can build an ellipse along its large AB and small CD axes (Fig. 37, a). On the axes of the ellipse as on the diameters build two circles, which can be divided by radii into several parts. Through the division points of the large circle, straight lines are drawn parallel to the minor axis of the ellipse, and through the division points of the small circle are straight lines parallel to the major axis of the ellipse. The points of intersection of these lines are the points of the ellipse.

We can give an example of constructing an ellipse with two conjugate diameters (Fig. 37, b ) MN and KL. Conjugate two diameters are called if each of them halves chords parallel to another diameter. A parallelogram is built on conjugate diameters. One of the diameters MN is divided into equal parts; The sides of the parallelogram, parallel to the other diameter, are also divided into the same parts, numbering them as shown in the drawing. From the ends of the second conjugate diameter KL , rays pass through the fission points. At the intersection of the same rays get the point of the ellipse.

A parabola is a non-closed curve of the second order, all points of which are equally removed from one point - the focus and from this straight line - the directrix.

Consider an example of constructing a parabola along its vertex O and some point B (Fig. 38, a). For this purpose, a rectangle OABC is built and its sides are divided into equal parts, rays are drawn from the fission points. At the intersection of the rays of the same name receive points of a parabola.

We can give an example of constructing a parabola in the form of a curve, a tangent line with points A and B given on them (Fig. 38 b). The sides of the angle formed by these straight lines are divided into equal parts and

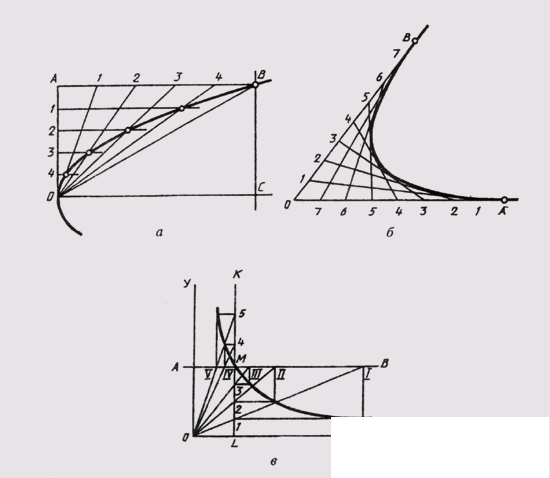
Fig. 38

measure the points of division. The points of the same name are connected by straight lines. The parabola is drawn as the envelope of these lines.

A hyperbola is a second-order, flat, unclosed curve consisting of two branches, the ends of which are removed to infinity, tending to their asymptotes. A hyperbola is distinguished by the fact that each point of it has a special property: the difference of its distances from two given points-foci is a constant value equal to the distance between the vertices of the curve. If the asymptotes of the hyperbola are mutually perpendicular, it is called equilateral. An equilateral hyperbole is widely used to construct various diagrams when one point M is specified with its coordinates (Fig. 38, c). In this case, through a given point, the lines AB and KL are drawn parallel to the coordinate axes. From the obtained points of intersection draw lines parallel to the coordinate axes. At their intersection, hyperbola points are obtained.

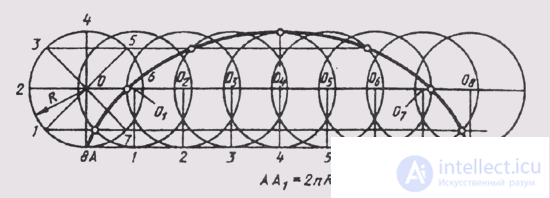
Fig. 39

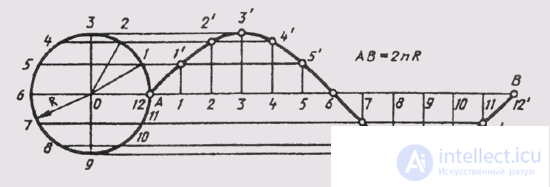
Fig. 40

A cycloid is a curve line that represents the trajectory of point A when a circle rolls over (fig. 39). To build a cycloid from the initial position of point A, lay off the segment AA], note the intermediate position of point A. So, at the intersection of the line passing through point 1 with the circle described from the center O ₁ , get the first point of the cycloid. Connecting the smooth straight line points, get cycloid.

A sine wave is a flat curve depicting a change in sine versus a change in its angle. To build a sine wave (Fig. 40), you need to divide the circle into equal parts and divide the straight line segment AB = 2лR into the same number of equal parts . From the same dividing points, draw mutually perpendicular lines, at the intersection of which receive points belonging to a sinusoid.

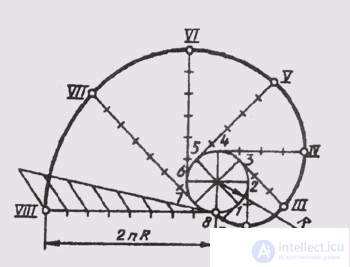
Fig. 41

An involute is a flat curve that is the trajectory of any point on a straight line that rolls around a circle without sliding. The construction of the evolvent is performed in the following order (Fig. 41): the circle is divided into equal parts; hold tangents to the circle, directed in one direction and passing through each point of the division; on a tangent line drawn through the last dividing point of a circle, lay a segment equal to the circumference of 2 liters R, which is divided into as many equal parts. On the first tangent lay one division of 2 liters of R / n , on the second - two, and so on.

The resulting points are joined by a smooth curve and get an involute circle.