24. The main elements of the geometric space

In engineering graphics, geometric space is considered as a set of homogeneous elements. The main shaping elements of the geometric space are points, lines (straight lines and curves), surfaces (flat and curves).

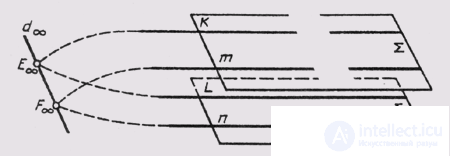
Fig. 42

Distinguish space Euclidean and non-Euclidean. Euclidean space is characterized by the fact that parallel straight lines or planes located in it do not intersect. The characteristics of the Euclidean space do not take into account a number of other geometric properties of space. In a broader understanding, these properties take into account the projective space in which straight lines (planes) parallel to each other intersect. These intersections occur at the so-called improper point, which is located at the infinity of the projective space. For example, we can give two parallel planes S and S ₁ (Fig. 42). Let us draw a line K in the plane S , and a line L in the plane Si, so that they are parallel. In projective space, these lines intersect outside their proper point E infinity. Further, in the plane S we draw a straight line m, and in the plane Si the straight line n so that they are parallel. These straight lines also intersect outside the proper point F infinity . It is easy to see that the improper points of E infinity and F infinity define the improper straight line d infinity . Taking into account that improper points belong to the plane S and the plane S ₁ , it can be argued that the improper straight line also belongs to these planes. Thus, we have the case when two parallel planes S and S ₁ intersect along an infinitely distant non-proper line d infinity .

The characteristics of the projective space allow in some cases to simplify the formulations adopted for the Euclidean space. This can be confirmed by the following example. In the axioms of Euclidean space, it is noted that two straight lines define a single point if they are not parallel. For projective space, the clause “if they are not parallel” loses its meaning.

In the conventional sense, space can be considered as infinite. However, the geometric space can be considered from the standpoint of dimension. Thus, the set of positions of a point moving in a given straight direction, forms an infinite straight line representing one-dimensional space. If the straight line is moved in a given direction, not parallel to the straight line itself, it forms an infinite surface (in this case, a plane), which is a two-dimensional space. By specifying a plane (surface) direction that is not parallel to it and moving it in this direction, we obtain three-dimensional space. In the same way, one can obtain a four-dimensional and in general form multidimensional space.

We adopt the following notation for space elements. Dots will be denoted by capital letters of the Latin alphabet: A, B, C ... or the numbers 1, 2, 3 ...; straight lines - lower case letters of the Latin alphabet: a, b, c ..., and planes - in capital letters of the Greek alphabet: G, L, P, S, F, ¥, Q.

Between the elements of space there are the following relationships.

This identity is denoted by ==, for example, A == B. This means that point A coincides with point B.

Incidence (or affiliation) is indicated by a?. For example, eh? a means that point A belongs to (incident) line a.

Parallelism is indicated by ||. For example, K || L means that straight line K is parallel to straight line.

Perpendicularity is indicated by _ | _ . For example, a _ | _ S means that the line a is perpendicular to the plane S.

Above the elements of the space, you can perform the connection operation , which is denoted by the sign and. For example, the record A and B ~ a means that as a result of connecting the points A and B a direct line a is obtained . Intersection is denoted by the symbol ^. The entry m ^ n = K means that the point K is obtained by intersecting the type line .