65. Building a line of intersection of surfaces by the method of auxiliary cutting planes

When constructing the line of intersection of two surfaces by the method of auxiliary cutting planes, the cutting planes taken as intermediaries can be of both a general and a particular position. More extensive use of find the plane of private position.

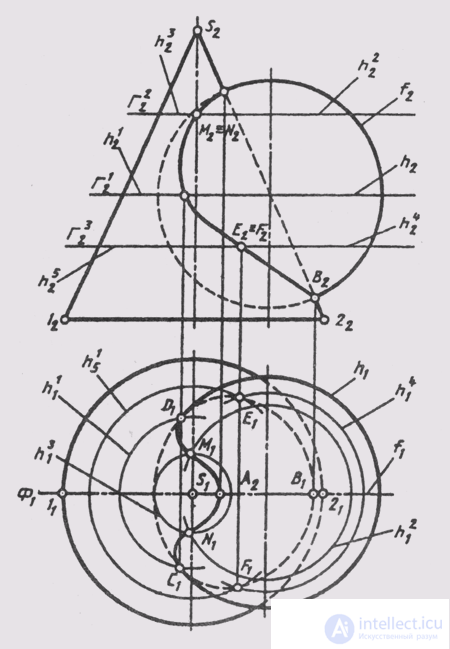
Fig. 132

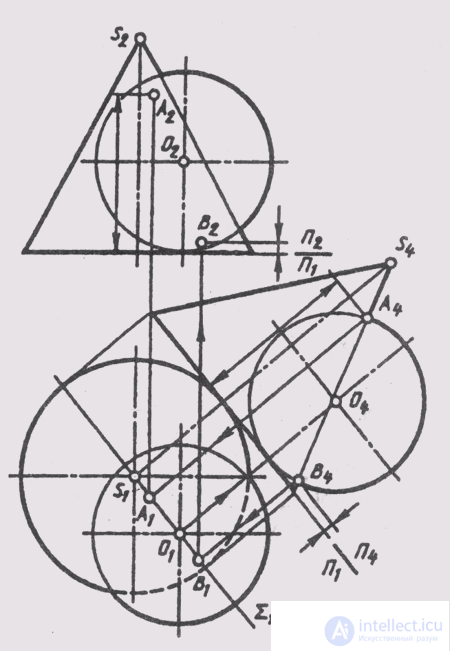
Fig. 133

The planes of general position apply in limited cases. For example, it is convenient to use them when constructing the line of intersection of conic and cylindrical, as well as general pyramidal and prismatic surfaces, when the bases of these surfaces are located in the same plane.

The solution of the problem of constructing the line of intersection of two surfaces by the method of auxiliary section planes is considered by the example of the intersection of a cone of rotation with a sphere. As intermediary surfaces we take the plane of a particular position — the horizontal level. In fig. 132 we first note the obvious common points A and B of the surfaces at the intersection of their main meridians f and 1 -S-2, since the surfaces have a common frontal plane of symmetry F (F ₁ ); f ₂ ^ S ₂ - S ₂ = A ₂ (B ₂ ); A ₂ A _l (B ₂ B _l ) || S ₂ S ₁ , A ₂ A _l (B ₂ B _l ) ^ f ₁ = A ₁ (B ₁ )

These reference points are the highest A and the lowest B points of the intersection line, as well as the points of visibility of the line on the plane P ₂ .

It is inconvenient to take auxiliary frontal planes parallel to П ₂ to construct the following points, since they will cross the cone along hyperbolas. Graphic simple lines (circles of parallels) on these surfaces are obtained from their intersection by horizontal planes of level G.

We take the first such auxiliary plane G ¹ at the equator level of the sphere I. This plane intersects the cone along the parallel h ¹ . In the intersection of these parallels are the point of view of the intersection line relative to the plane P ¹ :

h ¹ ^ h ¹ ₁ = C ₁ (D ₁ ); C ₁ C ₂ || S ₁ S ₂ ; C ₁ C ₂ ^ h ₂ (h ^l ₂ ) = C ₂ (D ₂ ).

If the intersecting surfaces of revolution do not have a common frontal plane of symmetry (Fig. 133), then the highest A and low B points of the intersection point of the surface are easily determined by plotting images of these surfaces on the plane P ₄ parallel to the axial plane Sum (Sum ₁ ) of these surfaces. You can construct the projections of the entire intersection line in the system of planes P ₁ _ | _ P ₄ , and then build its frontal projection in a projection connection with the horizontal projection, measuring the heights of points on the plane P ₄ , as shown in Fig. 132 for points A and B.