61. The intersection of a line with a plane

The line intersects the plane at one point. The point of intersection of the straight line with the plane is determined by constructing an auxiliary straight line lying in the same projecting plane with the given straight line. In fig. 119, and a complex drawing of a straight line l and a plane 9 (ABC) is shown , with m ~ Q (ABC). Through the horizontal projection of the straight line l ₁ we carry out the projection of the auxiliary horizontally projecting plane Sum ₁ . At the intersection of the planes Q and Sum we get the line t, that is, t = Sum ^ Q. The horizontal projection of the straight line t is determined by the horizontal projections of points 1 and 2 of the intersection of the EC and AC lines with the auxiliary plane Sum, that is, B ₁ C ₁ ^ Sum = l ₁ ; A ₁ C ₁ ^ Sum ₁ = 2 ₁ ; t ₁ = l ₁ ^ 2 ₁ .

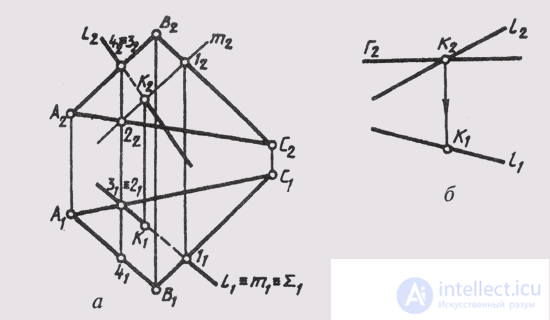
Fig. 119

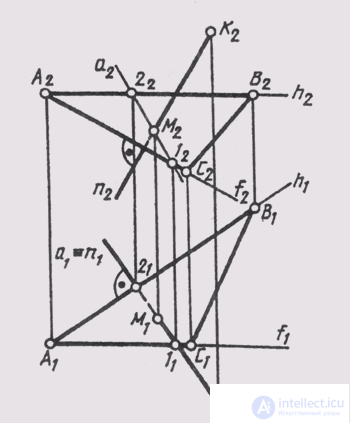
Fig. 120

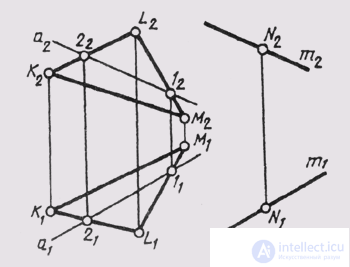
Fig. 121

To obtain the frontal projection of the line l, we construct the frontal projections of points 1 and 2, connecting which we obtain the frontal projection m ₂ . At the intersection of the frontal projections of the lines m and l, we obtain the frontal projection of the point K belonging to both the straight line l and the straight line m lying in the Sum plane. Therefore, the point K belongs to the Sum plane, and is the intersection point of the line l with the Sum plane.

The visibility of the straight line and the plane relative to the horizontal plane of the projections is determined using the horizontally competing points 2 and 3, and the visibility relative to the frontal plane of the projection is determined using the front-competing points 3 and 4.

If the plane occupies a particular position, then one projection of the point of intersection of the straight line with the plane is immediately determined at the intersection of the degenerate projection of the plane with the corresponding projection of the straight line (Fig. 119 b).

If a straight line intersects a plane at a right angle, then in the complex drawing, the projections of this straight line are perpendicular to the projections of the corresponding level lines of the plane based on the theorem on the projection of a right angle (see § 29).

In fig. 120 the projections of the base M of the perpendicular n, drawn to the plane 9 (ABC) from the point K of the space, are constructed. In A BC we have: AB - horizontal (A ₂ B ₂ _ | _ A ₂ A ₁ ), AC - frontal (A ₁ С ₁ _ | _A ₁ A ₂ ). Therefore, the projections of the perpendicular n e K are located: n ₁ _ | _A ₁ B ₁ and n ₂ _ | _ A ₂ С ₂ . The base of the perpendicular on the plane is constructed with the help of an auxiliary line and a plane lying in the same horizontal plane with the perpendicular n (a ^ n = M).

If a straight line intersects a plane at infinity, then there is a parallelism of a straight line with a plane. In fig. 121 a straight line t is drawn , passing through the point N u parallel to the plane of the triangle KLM. In a complex drawing, parallelism of a line and a plane is proved by the fact that m ₁ || a ₁ and m ₂ || a ₂ ; a ~ KLM.