66. Building a line of intersection of surfaces by the method of auxiliary spheres

When constructing the line of intersection of surfaces, the peculiarities of the intersection of coaxial surfaces of revolution allow using spheres co-axial with these surfaces as auxiliary intermediary surfaces.

By coaxial surfaces of rotation are surfaces having a common axis of rotation. In fig. 134 shows coaxial cylinder and sphere (fig. 134, a), coaxial cone and sphere (fig. 134, b) and coaxial cylinder and cone (fig. 134, c).

Coaxial surfaces of revolution always intersect along circles whose planes are perpendicular to the axis of rotation. There are as many of these circles common to both surfaces as there are intersection points of the outline lines of the surfaces. The surfaces in fig. 134 intersect in circles created by points 1 and 2 of the intersection of their main meridians.

The auxiliary sphere mediator intersects each of the given surfaces in a circle, at the intersection of which points are obtained that belong to the other surface, and hence the intersection lines.

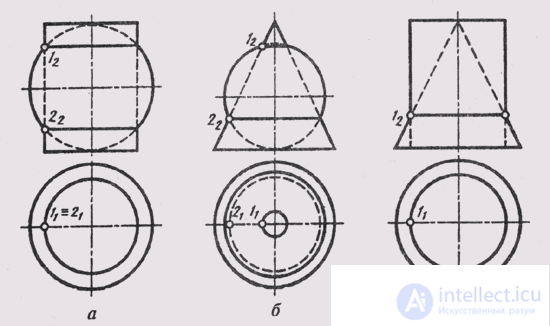
Fig. 134

If the axes of the surfaces intersect, the auxiliary spheres are drawn from one center-point of intersection of the axes. The line of intersection of the surfaces in this case is constructed by the method of auxiliary concentric spheres.

When building a line of intersection of surfaces to use the method of auxiliary concentric spheres, the following conditions must be met:

1) the intersection of the surfaces of revolution;

2) the axes of the surfaces — intersecting straight lines — are parallel to one of the planes of the projections, that is, there is a common plane of symmetry;

3) it is impossible to use the method of auxiliary cutting planes, since they do not give graphically simple lines on surfaces.

Usually, the method of auxiliary spheres is used in combination with the method of auxiliary cutting planes. In fig. 135 a line of intersection of two conical surfaces of revolution with axes of rotation intersecting in the frontal plane of the level F (F ₁ ) is constructed. This means that the main meridians of these surfaces intersect and give, in their intersection of the point of view, the intersection line relative to the plane P ₂ or the highest A and the lowest B point. In the intersection of the horizontal meridian h and parallel h ', lying in one auxiliary sectioning plane G (G ₂ ), the points of visibility C and D of the intersection line relative to the plane P _{1 are} determined . It is not advisable to use auxiliary cutting planes to build additional points of the intersection line, since planes parallel to Φ will intersect both surfaces along hyperbolas, and planes parallel to Γ will produce intersections of the surfaces of a circle and a hyperbola. Auxiliary horizontally or frontally projecting planes drawn through the top of one of the surfaces will intersect them along generators and ellipses. In this example, the conditions are met that allow the use of auxiliary spheres to construct the points of the intersection line. The axes of the surfaces of rotation intersect at the point O (O ₁ ; O ₂ ), which is the center of the auxiliary spheres, the radius of the sphere varies within

Rmin O of the most distant point B (R _max = О ₂ В ₂ ), and the radius of the minimum sphere is defined as the radius of the sphere touching one surface (along the circle h ² ) and intersecting the other ( circumference h ³ ).

The planes of these circles are perpendicular to the axes of rotation of the surfaces. At the intersection of these circles, we obtain points E and F belonging to the line of intersection of the surfaces:

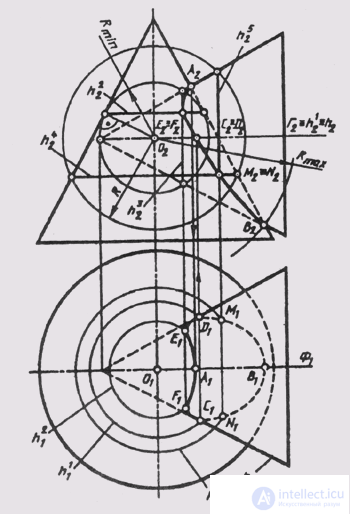
Fig. 135

h ² ₂ h ³ ₂ = E ₂ (F ₂ ); E ₂ E ₁ || A ₂ A ₁ ;

Е ₂ Е ₁ ^ h ² ₁ = E ₁ ; F ₂ F ^ h ₁ = F ₁

The intermediate sphere of radius R intersects the surface in circles h ⁴ and h ⁵ , at the intersection of which there are Mi points N:

h ⁴ ₂ ^ h ⁵ ₂ = M ₂ (N ₂ ); M ₂ M ₁ || A ₂ A ₁ ,

M ₂ M ₁ ^ h ⁴ ₁ = M ₁ ; N ₂ N ₁ ^ h ⁴ ₁ = N ₁

Connecting the similar projections of the constructed points with regard to their visibility, we obtain the projections of the line of intersection of the surfaces.