29. Orthogonal projections

Orthogonal (rectangular) projection is a special case of parallel projection, when all projecting rays are perpendicular to the projection plane. Orthogonal projections have all the properties of parallel projections, but with a rectangular projection, the projection of a segment, if it is not parallel to the plane of projections, is always smaller than the segment itself (Fig. 58). This is explained by the fact that the segment itself in space is the hypotenuse of a right-angled triangle, and its projection is the leg: А'В ' = ABcos a.

With rectangular projection, a right angle is projected life-size when both sides of it are parallel to the plane of projections, and then when only one of its sides is parallel to the plane of projections and the other side is not perpendicular to this plane of projections.

The theorem on the projection of a right angle. If one side of a right angle is parallel to the plane of projections, and the other side is not perpendicular

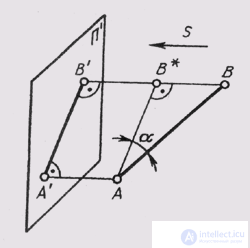
Fig. 58

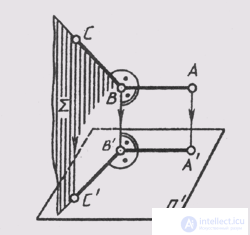
Fig. 59

when orthogonal projection, the right angle is projected onto this plane at the right angle.

Let a right angle ABC be given , for which the side AB is parallel to the plane n ' (fig. 59). The projecting plane is perpendicular to the plane n '. This means AB _ | _S , because AB _ | _ BC and AB _ | _ BB, hence AB _ | _ V'S '. But since kakAV || A'B ' _ | _ B'C', i.e. on the plane n 'the angle between A'B' and B'C is equal to 90 °.

Reversibility drawing. Projection onto one plane of projections gives an image that does not allow to unambiguously determine the shape and size of the depicted object. Projection A (see fig. 53) does not determine the position of the point itself in space, since it is not known how far it is from the plane of the projections n '. Any point of the projecting ray passing through point A will have point A 'as its projection . Having one projection creates an image uncertainty. In such cases, it is said that the drawing is irreversible, since it is impossible to reproduce the original in such a drawing. To eliminate uncertainty, the image is supplemented with the necessary data. In practice, various methods of supplementing a single-projection drawing are used. This course will deal with drawings obtained by orthogonal projection onto two or more mutually perpendicular projection planes (complex drawings) and by reproducing an auxiliary projection of the subject on the main axonometric projection plane (axonometric drawings).