54. Surfaces of rotation

The surfaces of revolution are those formed by rotating the line l around the straight line i, which is the axis of rotation. They may be ruled, such as a cone or cylinder of rotation, and non-linear or curvilinear, such as a sphere. The determinant of the surface of revolution includes the generator l and the axis i. The curvilinear surface of rotation is formed by rotating

Each point forming during rotation describes a circle whose plane is perpendicular to the axis of rotation. Such circles of the surface of revolution are called parallels. The largest of the parallels is called the equator. Equator. Determines the horizontal essay of the surface, if i _ | _ П ₁ . In this case, the parallels are the horizontal lines h   this surface.

Curved surfaces of revolution resulting from the intersection of the surface by planes passing through the axis of rotation are called meridians. All the meridians of one surface are congruent. The frontal meridian is called the prime meridian; he determines the frontal sketch of the surface of rotation. The profile meridian determines the profile sketch of the surface of revolution.

It is most convenient to build a point on curved surfaces of revolution with the help of parallel surfaces. In fig. 103 point M is built on parallel h ⁴ .

Surfaces of rotation found the widest application in the technique. They limit the surfaces of most engineering parts.

The conical surface of rotation is formed by rotating a straight line i around a straight line intersecting with it - the axis i (Fig. 104, a). The point M on the surface is constructed with the help of the generator l and the parallel h. This surface is also called a cone of rotation or a right circular cone.

The cylindrical surface of rotation is formed by rotating the straight line l around the axis i parallel to it (Fig. 104, b). This surface is also called a cylinder or a straight circular cylinder.

A sphere formed by rotating a circle around its diameter (Fig. 104, c). Point A on the surface of the sphere belongs to the principal

Fig. 103

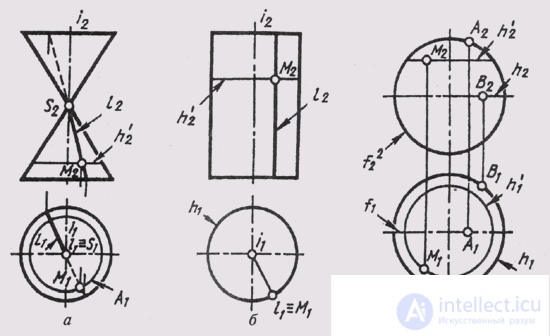
Fig. 104

the meridian f, point B - to the equator h, and the point M is built on the auxiliary parallel h '.

A torus is formed by rotating a circle or its arc around an axis lying in the plane of the circle. If the axis is located within the formed circle, then such a torus is called closed (Fig. 105, a). If the axis of rotation is outside the circle, then such a torus is called open (Fig. 105, b). An open torus is also called a ring.

Surfaces of revolution can also be formed by other curves of the second order. The ellipsoid of rotation (Fig. 106, a) is formed by rotating an ellipse around one of its axes; paraboloid of rotation (fig. 106, b) - rotation of the parabola around its axis; A single-cavity hyperboloid of rotation (Fig. 106, c) is formed by rotating a hyperbola around the imaginary axis, and a two-cavity hyperboloid (Fig. 106, d) is formed by rotating a hyperbola around the real axis.

In the general case, surfaces are depicted as not limited in the direction of propagation of the forming lines (see figs. 97, 98). To solve specific problems and obtain geometric shapes are limited to the planes of the crop. For example, in order to obtain a circular cylinder, it is necessary to limit the portion of the cylindrical surface to the planes of the cut (see Fig. 104, b). As a result, we obtain its upper and lower bases. If the cutting planes are perpendicular to the axis of rotation, the cylinder will be straight, if not, the cylinder will be inclined.

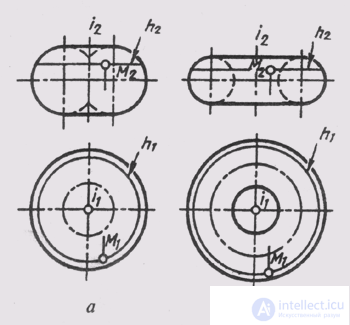
Fig. 105

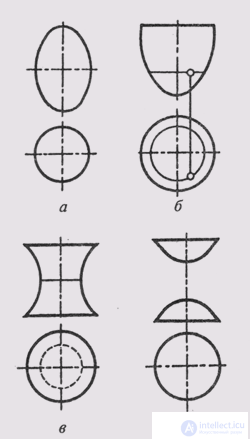
Fig. 106

To get a circular cone (see fig. 104, a), it is necessary to cut along the top and beyond. If the cutting plane of the cylinder base is perpendicular to the axis of rotation, the cone will be straight, if not, it will be inclined. If both cutting planes do not pass through the top - the cone will get truncated.

Using the plane of the crop, you can get a prism and a pyramid. For example, a hexagonal pyramid will be straight if all its edges have the same inclination to the trimming plane. In other cases, it will be inclined. If it is made using cutting planes and none of them passes through the top, the pyramid is truncated.

A prism (see fig. 101) can be obtained by limiting a portion of the prismatic surface to two planes of the crop. If the cut plane is perpendicular to the edges, for example, an octagonal prism, it is straight, if not perpendicular, it is inclined.

By choosing the appropriate position of the cutting planes, one can obtain various forms of geometric shapes depending on the conditions of the problem being solved.