43. Curves

Curves in the complex drawing set their projections, which are built on the projections of individual points belonging to this line. Projections of lines when orthogonal projection is obtained as a result of the intersection of the projecting cylinders with the planes of the projections (see § 28); This means that the projections of flat and spatial curved lines are flat lines. In fig. 79 it can be seen that the secant m curve a is generally projected to the secant of its projection, and the tangent / to the curve is projected to the tangent to its projection.

In a complex drawing of a curve, its singular points, which include the points of inflection, return, break, and anchor points, are also special points on its projection. This is explained by the fact that singular points of curves are connected with tangents at these points.

If the plane of the curve takes a projecting position (Fig. 80, a), then one projection of this curve has the shape of a straight line. A spatial curve has all its projections - curved lines (Fig. 80, b).

In order to establish in the drawing which curve is set (flat or spatial), it is necessary to find out whether all points of the curve belong to the same plane. Set in fig. 80, b curve is spatial, as the point D of the curve does not belong to the plane defined by three other points A, B and E of this curve.

Construction and the image of curves was considered in § 21,22, therefore we will give an example of the image on the drawing only a circle as a flat curve and a helix as a spatial curve.

A circle is a plane curve of the second order, the orthogonal projection of which can be a circle and an ellipse (Fig. 81, a). For the image of a circle of diameter d in the complex drawing, one must construct projections of the center O and its two diameters. It is most convenient to build projections of diameters parallel to the planes of the projections: AB || P ₁ CD || P ₂ ; CD _ | _ P ₁ (fig. 81, b). The frontal projection of a circle - an ellipse - is determined by the small axis of the ellipse A ₁ B ₂ = dcos b and the major axis of the ellipse C ₂ D ₂ = d

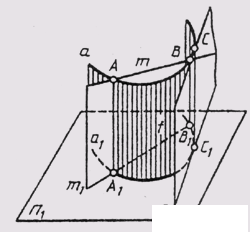
Fig. 79

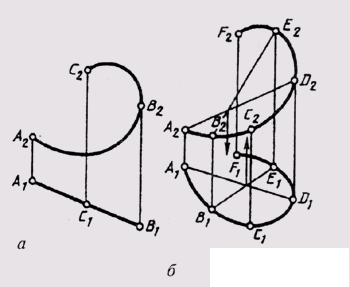
Fig. 80

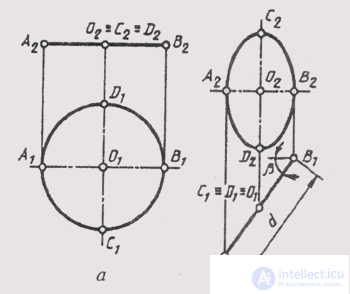
Fig. 81

If the plane of the circle is inclined to all the main planes of the projections, then all three of its projections are ellipses that can be constructed from conjugate diameters, which are the projections of those diameters of a circle that are parallel to the planes of the projections (see. 37).

A cylindrical helix (gel) is a spatial curve representing the trajectory of a point performing a helical motion. The screw movement includes a uniform translational motion of a point along a straight line and a uniform rotational movement of this straight line with a point around the axis i, in which the straight line is parallel. The height p, to which a point rises in a straight line for a full revolution, is called the helix pitch (Fig. 82). If the axis i of the helix is ​​perpendicular to the horizontal plane of the projections, then the horizontal projection of the helix is ​​a circle, and the frontal one is a sinusoid.

To construct the frontal projection of the helix at a given diameter d and step p, it is necessary to divide both the circle and the step into an equal number of parts. The projection of the helix point is shown in fig. 82. The cylindrical screw line can be turned

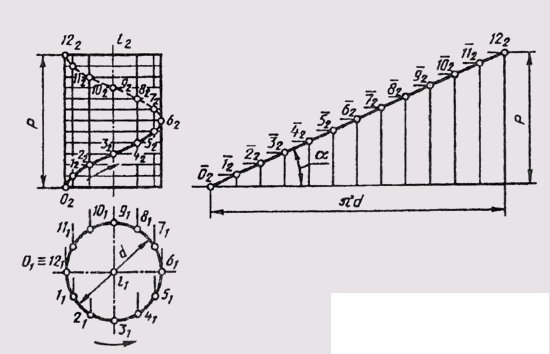
Fig. 82

on the plane. Its development is a straight line with an angle of elevation a, where tga = P / ld.