52. Faceted surfaces

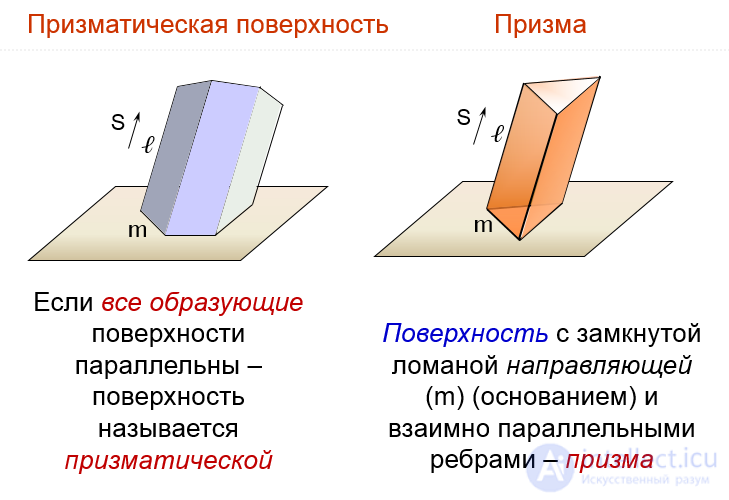
Faced surfaces are those formed by moving a straight line generator l along a broken guide m. Moreover, if one point S of the generator is fixed, a pyramidal surface is created (Fig. 97), if the generator is parallel to the specified direction S when moving , then a prismatic surface is created (Fig. 98).

The elements of the face surfaces are: the vertex S (at the prismatic surface it is at infinity), the face (the part of the plane bounded by one section of the guideline m and the extreme relative to it by the positions of the generator l) and the edge (the line of intersection of adjacent faces).

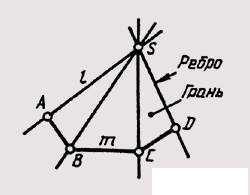
Fig. 97

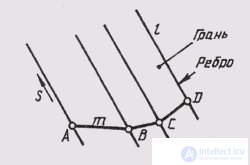
Fig. 98

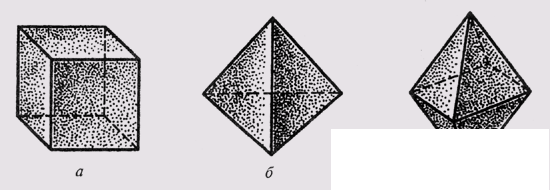
Fig. 99

The determinant of the pyramidal surface includes the vertex S, through which the generators and guides pass: l '~ S;

l ^ t.

The determinant of a prismatic surface, in addition to the guide t, contains the direction S, to which all the surfaces that form l are parallel: l || S; l ^ t.

Closed faceted surfaces formed by a certain number (at least four) faces are called polyhedra. Among polyhedrons, a group of regular polyhedrons is distinguished, in which all faces are regular and congruent polygons, and polyhedral angles at the vertices are convex and contain the same number of faces. For example: a hexahedron is a cube (Fig. 99, a), a tetrahedron is a regular quadrilateral (Fig. 99, 6). The octahedron is a polyhedron (Fig. 99, c). Crystals have the shape of various polyhedra.

The pyramid is a polyhedron, at the base of which is an arbitrary polygon, and the lateral faces are triangles with a common vertex S.

In a complex drawing, a pyramid is defined by the projections of its vertices and edges, taking into account their visibility. The visibility of the edge is determined using competing points (Fig. 100).

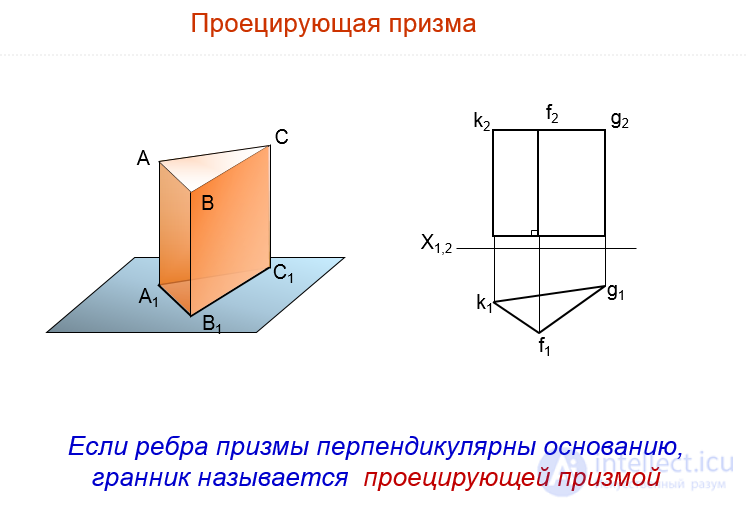
A prism is a polyhedron whose base is two identical and mutually parallel polygons, and its side faces are parallelograms. If the edges of the prism are perpendicular to the plane of the base, such a prism is called a straight line. If a prism has an edge perpendicular to any plane of projections, then its side surface is called projecting. In fig. 101 is given a complex drawing of a straight quadrilateral prism with a horizontally projecting surface.

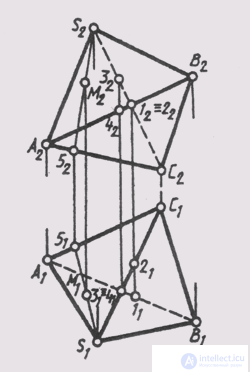
Fig. 100

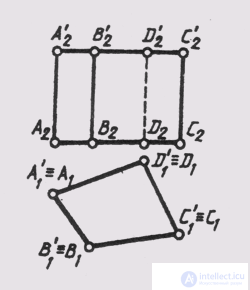
Fig. 101

When working with a complex drawing of a polyhedron, it is necessary to build lines on its surface, and since a line is a collection of points, it is necessary to be able to build points on the surface.

Any point on a faceted surface can be constructed using a generator passing through this point. In fig. 100 in the face of ACS , point M is constructed by means of S-5 generator .