44. The mutual arrangement of points and lines.

A point in space with respect to the line can occupy two positions: to belong to it or not to belong. If it belongs to a line, it forms a whole with it and its projections on the drawing lie on the corresponding projections of the line, as well as on one communication line.

If at least one of the projections of a point does not lie on the projection of the line, the point does not belong to it. In fig. 83 shows a complex drawing of the line l, as well as a series of points. It can be seen from the drawing that point A belongs to line b , since its horizontal projection A ₁ lies on the horizontal projection of line 1 ₁ , and the front projection of point A ₂ is located on the frontal projection of line A and

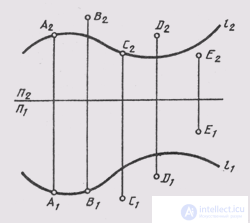
Fig. 83

lives on the same vertical communication line with point А ₁ . Points B and C do not belong to line l , since they are frontal in the first one, and do not belong to corresponding projections in the second horizontal projection. The points D and E do not belong to the line l , since none of their projections belong to the corresponding projection of the line.