70. Determination of the true value of angles

The task of determining the true magnitude of the angles (planar) is more convenient to solve by converting the original drawing by rotating around the level line. The true magnitude of the angles between intersecting straight lines c and d (Fig. 143) is determined as follows: the angle plane is rotated around its frontal f (1, 2) to align it with the frontal plane of the level F (F ₁ ) passing through

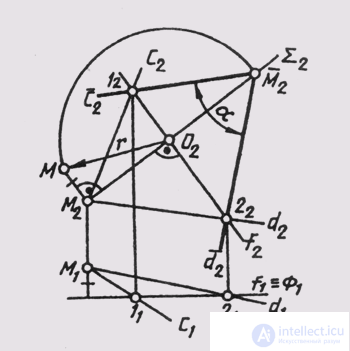
Fig. 143

frontal f The MI projection of the overlap of the vertex M of the angle between the lines c and d is on the Sum 2 projection of the frontally projecting Sum plane in which the point M rotates . Having determined with the help of a right triangle O ₂ M ₂ M, the actual size of the radius of rotation r and putting it on the projection E ₂ from the frontal projection of the center of rotation, we obtain an image of the point M on the plane P ₂ in the position combined with the plane F. Connecting the frontal projections of the fixed points 1 and 2 with the constructed point M, we obtain the projections with ₂ and d ₂ combined with the plane F of the straight lines c and d. The angle between straight lines c ₂ and d ₂ determines the actual size of the desired angle between intersecting straight lines c and d.

This task can also be solved by replacing the projection planes. To do this by double replacing the planes of the projections, you need to make the plane of the angle a plane of the level, deciding successively, first the third original problem, and then the fourth one.

The natural angle between intersecting straight lines is defined as the angle between two intersecting straight lines parallel to the given intersecting straight lines.

The angle a between the straight line l and the plane 6 can be determined through an additional angle p between the given straight line l and the perpendicular n to this plane drawn from any point of the straight line (Fig. 144). Angle P complements the desired angle a to 90 °. Having determined the true value of the angle P by rotating around the straight level of the plane the angle formed by the straight line l and the perpendicular u, it remains to add it to the right angle. This additional angle will give the true value of the angle a between the straight line l and the plane 0.

The true value of the dihedral angle is between two planes Q and l. - can be determined either by replacing the projection plane to convert the edge of the dihedral angle into the projecting line (tasks 1 and 2), or if the edge is not specified as the angle between two perpendiculars n ¹ and n ² drawn to these planes (see § 61) from an arbitrary point M of space (see fig. 145). In the plane of these perpendiculars at the point M we get two flat

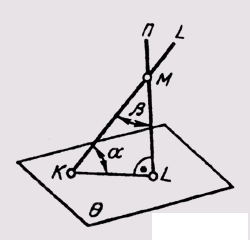
Fig. 144

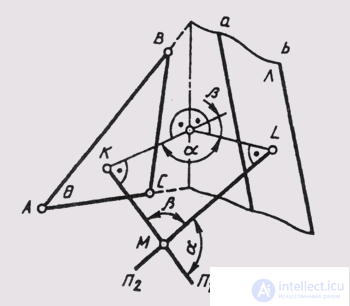
Fig. 145

angles a and P, which are respectively equal to the linear angles of two adjacent angles (dihedral), formed by the planes q and l ,. Having determined the true magnitude of the angles between the perpendicular n ¹ and n ² by rotating around a straight level, we also determine the linear angle of the dihedral angle formed by the q and l planes.