QUESTIONS FOR SELF-TESTS In descriptive geometry with answers

1. How to split a segment in half?

we find the middle of the segment whose ends A and B are given, with the help of one compass - without conducting the segment itself. Here is the solution to this problem. We describe a circle of radius AB with center B and on it, starting from A, as before, we measure out successively three arcs of radius AB. The last point C will lie on the line AB, and we will have: AB = BC. Then we describe a circle of radius AB with center A and construct a point C ', the inverse of C with respect to this circle. Then we get:

AC '* AC = AB2,

AC '* 2AB = AB2,

2AC = AB.

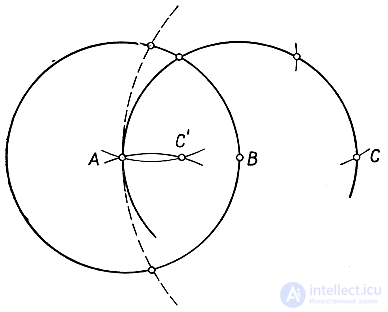
Fig. 44. Finding the middle of the segment

Hence, C is the desired midpoint of the segment.

2. How to divide a circle into four, eight, twelve parts?

Terms for circle constructions

A circle is a closed curve line, each point of which is located at the same distance from one point O, called the center.

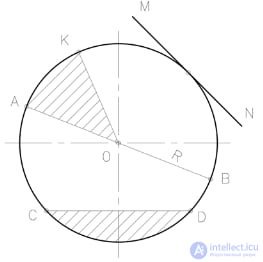
The straight lines connecting any point of the circle with its center are called the radii R.

The straight line AB connecting two points of the circle and passing through its center O is called the diameter D.

Parts of circles are called arcs.

The line CD connecting two points on a circle is called a chord.

A line MN that has only one common point with a circle is called a tangent.

The part of the circle bounded by the CD chord and the arc is called the segment.

The part of the circle bounded by two radii and an arc is called a sector.

Two mutually perpendicular horizontal and vertical lines intersecting in the center of the circle are called the axes of the circle.

The angle formed by the two radii of the KOA is called the central angle.

Two mutually perpendicular radii make an angle of 900 and limit 1/4 of the circle.

Division of a circle into 4 and 8 identical parts

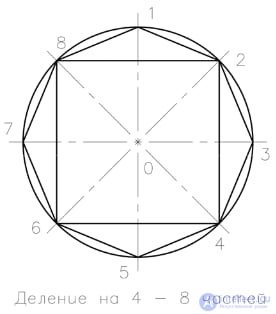
Draw a circle with horizontal and vertical axes that divide it into 4 equal parts. Drawn with a compass or square at 450, two mutually perpendicular lines divide the circle into 8 equal parts.

---

Division of a circle into 3 and 6 equal parts (multiples of 3 three)

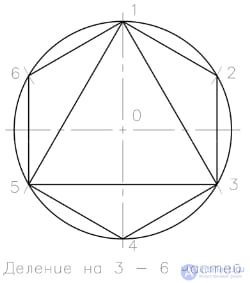
To divide the circle into 3, 6 and a multiple of the number of parts, draw a circle of a given radius and the corresponding axis. Division can begin from the intersection of the horizontal or vertical axis with the circle. The given radius of the circle is sequentially delayed 6 times. Then the obtained points on the circle are successively connected by straight lines and form a regular inscribed hexagon. Connecting points through one gives an equilateral triangle, and dividing the circle into three equal parts.

---

Division of a circle into 5 and 10 equal parts

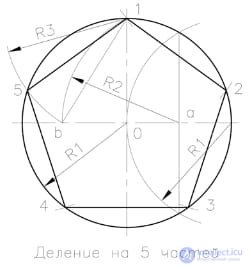
The construction of a regular pentagon is as follows. We draw two mutually perpendicular axis of the circle equal to the diameter of the circle. Divide the right half of the horizontal diameter in half using the arc R1. From the obtained point "a" in the middle of this segment of radius R2, draw an arc of a circle until it intersects with the horizontal diameter at point "b". A radius R3 from point "1" draws an arc of a circle until it intersects with a given circle (v.5) and get the side of a regular pentagon. The distance "b-O" gives the side of the regular decagon.

---

Division of a circle by the Nth number of identical parts (building a regular polygon from N sides)

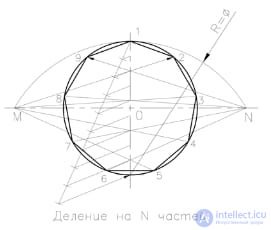
It is carried out as follows. We draw horizontal and vertical mutually perpendicular axis of the circle. From the upper point "1" of the circle, draw a straight line at an arbitrary angle to the vertical axis. On it we lay aside equal segments of arbitrary length, the number of which is equal to the number of parts by which we divide the given circle, for example 9. We connect the end of the last segment with the lower point of the vertical diameter. We draw lines parallel to the one drawn from the ends of the delayed segments until they intersect with the vertical diameter, thus dividing the vertical diameter of the given circle into a given number of parts. With a radius equal to the diameter of the circle, from the lower point of the vertical axis we draw the arc MN to the intersection with the continuation of the horizontal axis of the circle. From points M and N, we draw rays through the even (or odd) dividing points of the vertical diameter to the intersection with the circle. The obtained segments of the circle will be the desired ones, because points 1, 2, .... 9 divide the circle into 9 (N) equal parts.

3. Expand the principle of constructing rounding corners.

The conjugation of two intersecting straight lines by an arc of a given radius is called the rounding of the corners . Its implementation can be seen in Fig. 32. In parallel to the sides of the angle formed by these lines, auxiliary lines are drawn at a distance equal to the radius. The intersection point of the auxiliary lines is the center of the conjugation arc.

Perpendiculars are lowered from the obtained center O to the sides of a given angle, and at their intersection, the conjugation points A and A 'are obtained. Between these points spend a mating arc of radius R from the center of O.

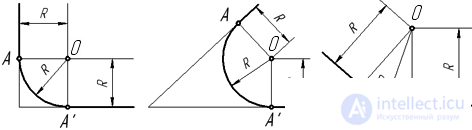
Fig. 32

Right angle fillet

The rounding of a right angle having a vertex O by an arc of radius R is carried out in the following sequence: 1. From the peak O draw an arc with a given radius R, until it intersects the sides of the angle at points A and B (mating points); 2. The center of the fillet O1 must be located at the geometrical location of the points equidistant from the sides of the angle, on the bisector of the angle AOW and is determined by the point of intersection of arcs of radius R drawn from the conjugation points A and B; 3. Draw an arc AB of radius R and center O1.

Acute angle fillet

Rounding an acute angle with an arc of radius R can be performed in the following sequence: 1. The geometric place of the points equidistant from the sides of the angle will be straight lines parallel to the sides of the angle and passing from them at a distance R; 2. The intersection point of these lines defines the center of fillet O1; 3. The intersection of the perpendiculars omitted from the center of the fillet with the sides will determine the position of the conjugation points A and B; 4. Move the arc AB from the center O1 of radius R.

Rounding an obtuse angle

Rounding an obtuse angle is exactly the same as a sharp one. You can slightly change the course of construction, if you use the angle bisector: 1. Build an angle bisector; 2. Draw a straight line parallel to one of the sides of the corner and spaced from it at a distance R; 3. The intersection point of this line with the bisector determines the position of the center of fillet O1; 4. The intersection of the perpendiculars omitted from the center of the fillet with the sides will determine the position of the mating points A and B; 5. Move the arc AB from the center O1 of radius R.

4. What is pairing?

5. What types of pairing do you know?

Conjugation is a smooth transition along a curve from one line to another. Pairings are circular and circular. Their construction is based on the properties of tangents to curved lines. Conjugation of line segments with compass curves will be possible if the conjugation point is simultaneously the point of tangency of the line to the arc of the curve. Consequently, the mating radius should be perpendicular to the line at the point of contact. The conjugation of circular curves is possible when the conjugation point is at the same time the tangent point of the mating arcs. Therefore, the point of tangency should be on the line of centers of the arcs of circles. The intersection of intersecting lines: Example 1 The intersecting straight lines AB and BC and the conjugation radius R are given; it is required to perform pairing of lines (Fig. 66, a, b, c). Conjugation will be possible if the lines AB and BC are tangent to a circle of radius R. To find the center of this circle it is necessary to draw auxiliary lines at a distance R parallel to the given lines until they intersect at point 0. From point O, as from the center, an arc of radius R is drawn. The mating points are points M and H, defined by the intersection of lines AB and BC with perpendiculars dropped from point O. Example 2 The intersecting straight lines AB and BC and the conjugation radii R and R1 are given. Conjugation is possible if the angle a <90. A method of constructing such a pair is shown in FIG. 66, g. Conjugation of parallel lines Example 1. Given two parallel lines AB and CE and the interface points B and C (Fig. 67). It is necessary to construct a smooth conjugation with circular curves so that it passes through a given point K, in the middle of the segment BC. To determine the radii and centers of the conjugation arcs, we divide the segments BK and KS straight so that they are perpendicular to these segments and divide them in half. Since the radius of the conjugation must be perpendicular to the straight line at the point of conjugation, to find the centers of the arc of conjugation, we restore the perpendiculars from points B and C to intersect them with the previously drawn perpendiculars to the direct line BC. The intersection points of these perpendiculars will determine the position of the O – O conjugation centers, and equal segments 05 and OC will give the values ​​of the conjugation radii. Example 2 (Fig. 68), This example is different from the previous one. the fact that the point K is taken on the line BC arbitrarily, at a certain distance e from the line CE; consequently, the conjugation radii R and R1 are different in magnitude. The course of constructing the mates is the same as in the previous example. P p and m ep 3 . Given: the distance between two parallel lines AB and CE, equal to the sum of the mating radii R and R1, and the interface point B (Fig. 69). To build a pair, draw an auxiliary straight line 0–01 parallel to AB at a distance R. The center of conjugation 0 for radius R will be at the intersection of the perpendicular drawn from point B to the auxiliary line. Describing from the point O an arc of radius R, we find the point K, from which with a radius R1 we make a notch on the auxiliary direct line that defines the center of conjugation O1. From point O1 we lower the perpendicular to the line CE and, finding the conjugation point C, we conjugate the points K and C with an arc of radius R1. Pairing a circular arc with a straight line Example 1. We construct a conjugation of an arc of radius R with a line AB of radius R1 (Fig. 70). To do this, find the center of conjugation 0 and the conjugation point C and a. Point C is at the same time their point of contact and must lie on the line of centers of these arcs. The mating radius should be perpendicular to the line AB at the point of tangency a. Therefore, from the center O we describe the arc equal to the sum R + R1. It will have the center of conjugation 0, to determine which we draw parallel to AB at a distance R1 its auxiliary line to the intersection with the drawn arc. Connecting the points O1 and O, we find the conjugation point C. To determine the point a, we omit the perpendicular from O1 to AB. Next, with a radius R1 from the center O1 we conjugate the points a and C. Example 2. Given: an arc of radius R, a straight line AB and a conjugation point a. It is required to find the mating point C and the mating radius R1 (Fig. 71). Draw the perpendicular to AB through point a, on which we lay down the segment aK equal to R. Connect the center O to point K. To find the center of conjugation O1, draw a perpendicular line through the middle of the segment OK, which intersects the line aK at point O1 Connecting O1 with O , find the conjugation point C. Match arc of circles with an arc of a circle The conjugation of the arcs of circles can be external (Fig. 72) or internal (Fig. 73). In both cases, the conjugations are feasible: 1) if the distance C between the centers O and 01 of the mating arcs is greater than the sum of their radii R and R1 (Fig. 72, a and 73, a), i.e. C> R + R1 and 2) when C = C + R1 or R1> = C + R is obtained. For external conjugation of arcs, conjugation will also be impossible if the radius of the conjugating arc R2 is less than the half-difference C - (R + R1), i.e., R2 < <(C- (R + R1)) / 2. In all cases, the solution of the problem reduces to finding the center 02 of the conjugate arc of radius R2 and the conjugation points A and B. External pairing. Given: arcs of radii R and R1, the distance C between the centers of these arcs and the radius of conjugation R2 (Fig. 72, a). It is required to construct conjugation provided that C> R + R1. To construct the conjugation, it is necessary to determine the center 02 and the conjugation points A and B. To find the center 02, draw an arc of radius R2 + R from the center О, and an arc of radius R2 + R1 from the center О1. The intersection of these arcs will determine the center 02. Connect the centers О and 01 by straight lines with center 02, we find at the intersection of these lines with the corresponding arcs the conjugation points A and B. The resulting points are mated with a radius of R2. Constructing for the case when C Internal pairing. Given: arcs of radii R and R1, the distance C between the centers of these arcs and the radius of conjugation R2 (Fig. 73, a). It is required to construct a conjugation if C> R + R1. The solution to this problem is the same as the previous one, with the only difference being that from the centers O and O1 arcs of radii R2 - R and R2 - R1 are drawn. In FIG. 73, b, the construction of conjugation is given for the case when C

6. What elements determine the pairing?

7. What second-order curves do you know?

A general second-order equation is an equation of the form:

Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0

where the coefficients A, B, C are simultaneously non-zero.
The lines defined by such equations are called second-order curves .
The center of a line is a point on the plane with respect to which the points of this line are arranged symmetrically in pairs.
Second-order lines with a single center are called center lines.
The coordinates of the center S (x0; y0) of the line are determined from the system:

Denote by .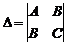
For Δ ≠ 0, the second-order curve will be central.
Moreover, for Δ> 0, the equation is an elliptic type equation. Each elliptic equation is an equation of either an ordinary ellipse, or a degenerate ellipse (point), or an imaginary ellipse (in this case, the equation does not define any geometric image on the plane).
For Δ <0, the equation is an equation of hyperbolic type . Each hyperbolic equation defines either an ordinary hyperbola or a degenerate (a pair of intersecting lines).
At Δ = 0, the second-order line is not central. Such equations are called parabolic type equations and define either an ordinary parabola on a plane or a pair of parallel (or coincident) lines, or they do not define any geometric image on a plane
Classification of second-order curves:

• Ellipse
• Circle
• Hyperbola
• Parabola

Optical properties of second-order curves:

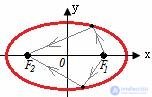
For an ellipse : rays of light emanating from one focus of the ellipse pass through the second focus after mirror reflection from the ellipse.

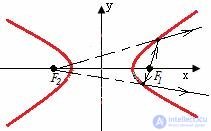
For hyperbole : the continuation of the reflected ray of light emanating from one focus of the hyperbola falls into the second focus.

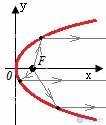
For a parabola: the rays of light emanating from the focus of the parabola, after specular reflection from it, form a bunch of rays parallel to its focal axis.

The equation in polar coordinates.
The polar equation, general in form for an ellipse, one branch of a hyperbola and a parabola, has the form:

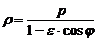
where φ, ρ are the polar coordinates of an arbitrary point on the line, p is a parameter, ε is the eccentricity. In this case, the polar coordinate system is selected as follows: the pole is in focus, the polar axis is directed in the direction opposite to the directrix closest to this focus.
In particular, for ε = 0, we obtain the equation of the circle in polar coordinates:
ρ = R

8. What is an oval?

Oval

An oval is a closed box curve having two axes of symmetry. A box curve is a one-sided convex closed or open line consisting of conjugate arcs of circles of different radii. Many parts of machines, instruments, and apparatuses have a contour outline, consisting of straight lines and arcs of circles with smooth transitions from one line to another.

9. Define the curve curves.

Patterned curves are plane curves drawn with patterns using previously constructed points. To the curves include: ellipse, parabola, hyperbola, cycloid, sinusoid, involute, etc.

10. Expand the principles of constructing an ellipse.

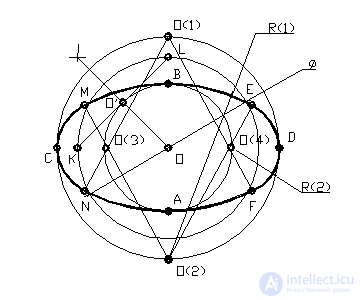
An ellipse is a closed plane curve of the second order. It is characterized by the fact that the sum of the distances from any of its points to two focal points is a constant value equal to the larger axis of the ellipse. There are several ways to build an ellipse. For example, you can build an ellipse along its large AB and small CD axes (Fig. 37, a). On the axes of the ellipse, as on the diameters, two circles are built, which can be divided by radii into several parts. Through the dividing points of the large circle draw straight lines parallel to the small axis of the ellipse, and through the dividing points of the small circle draw straight lines parallel to the major axis of the ellipse. The intersection points of these lines are the points of the ellipse.

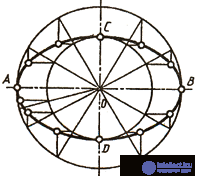
Fig. 37, and

We can give an example of constructing an ellipse from two conjugate diameters (Fig. 37, b) MN and KL. Paired two diameters are called if each of them bisects chords parallel to another diameter. A parallelogram is built on the conjugated diameters. One of the diameters MN is divided into equal Parts; the sides of the parallelogram parallel to another diameter are divided into the same parts, numbering them, as shown in the drawing. From the ends of the second conjugated diameter KL, rays are drawn through the division points, at the intersection of which ellipse points are obtained.

11. What curve is called a parabola?

A parabola is called an open curve of the second order, all points of which are equally distant from one point - the focus and from the straight line - the directrix.

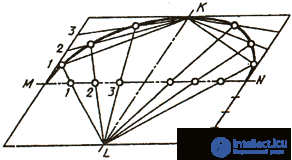
Let us consider an example of constructing a parabola at its vertex O and at any point B (Fig. 38, a). For this purpose, an OABS rectangle is built and its sides are divided into equal parts, rays are drawn from the division points. At the intersection of the rays of the same name, parabola points are obtained.

Fig. 38, and

We can give an example of constructing a parabola in the form of a curve tangent to straight lines with points A and B given on them (Fig. 38, b). The sides of the angle formed by these lines are divided into equal parts and the points of division are numbered. Points of the same name are connected by straight lines. A parabola is drawn as an envelope of straight lines.

12. What curve is called a hyperbole?

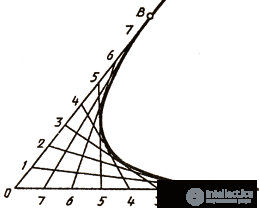
A hyperbola is called a flat open curve of the second order, consisting of two branches, the ends of which move to infinity, striving for their asymptotes. Hyperbola is distinguished by the fact that each point of it has a special property: the difference in its distances from two given focus points is a constant value equal to the distance between the vertices of the curve. If the asymptotes of a hyperbola are mutually perpendicular, it is called isosceles. An equal-sided hyperbole is widely used to construct various diagrams when one point M is given by its coordinates (Fig. 38, c). In this case, through the given point, the lines AB and KL are drawn parallel to the coordinate axes. From the obtained intersection points, lines are drawn parallel to the coordinate axes. At their intersection, hyperbola points are obtained.

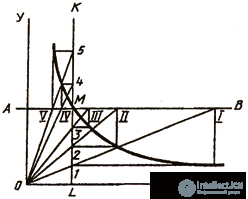
Fig. 38 in

13. Give a definition of cycloid.

Fig. 38 in

A cycloid is called a curved line representing the trajectory of point A when rolling a circle (Fig. 39). To build a cycloid from the initial position of point A, lay off the segment AA1, mark the intermediate position of point A. So, at the intersection of a straight line passing through point l with a circle described from the center O1, we get the first point of the cycloid. Connecting the smooth line of the constructed points, Get a cycloid.

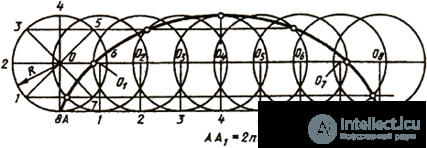
Fig. 39

14. Expand the principles of building a sinusoid.

A sinusoid is called a flat curve depicting a change in the sine depending on a change in its angle. To build a sinusoid (Fig. 40), you need to divide the circle into equal parts and divide the straight line segment AB = 2nR into the same number of equal parts. From the same division points, draw mutually perpendicular lines, at the intersection of which receive points belonging to a sinusoid.

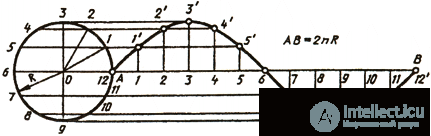
15. What is a flat curve called involute?

An involute is a plane curve that is the trajectory of any point on a straight line that rolls around a circle without slipping. The construction of involutes is performed in the following order (Fig. 41): the circle is divided into equal parts; draw tangents to the circle, directed in one direction and passing through each point of division; on a tangent drawn through the last point of division of the circle, lay out a segment equal to the circumference of 2πR, which is divided into as many equal parts. On the first tangent, one division 2πR / n is plotted, on the second - two, etc. The resulting points are connected by a smooth curve and an involute of a circle is obtained.

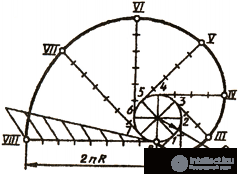
Fig. 41

Share article