41. The mutual arrangement of two straight

Two straight spaces can have a different location (Fig. 74). They can coincide a = b, be parallel c || d, intersect t ^ n and interbreed (k ° / l).

If two straight lines are parallel, then on the complex drawing (fig. 75, a) their like projections are parallel.

If two straight lines intersect at some point M, then the projections of this point should belong to the same projections of straight lines, that is, the intersection points of the same projections of intersecting straight lines should lie on the same communication line (Fig. 75 b):

m ^ n = M -> {m ₁ ^ n ₁ = M ₁ or m ₂ ^ n ₂ = M ₂ }

If two straight lines intersect, their projections of the same name can intersect at points not lying on the same communication line (Fig. 75, c):

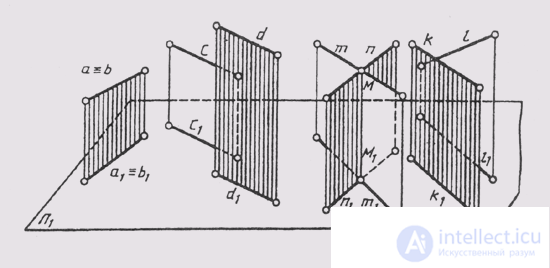
Fig. 74

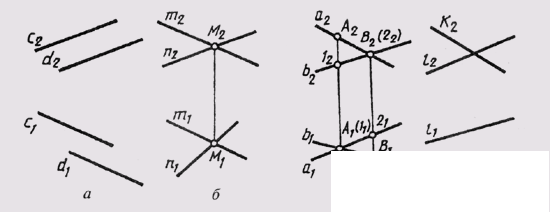
Fig. 75

a ° / b -> a ₁ ^ b ₁ = А ₁ (l ₁ ) - horizontally competing points; a ₂ ^ b ₁ = B ₂ (l ₁ ) are frontally competing points. In another case, one pair of projections will intersect, and the second can be parallel straight lines (Fig. 75, d):

k ⁰ / l -> {k ₂ ^ l ₂ or k ₁ || l ₁ }

Attention should be paid to special cases of determining the relative position of two straight lines in space. If one of them (Fig. 76, a) or both (Fig. 76, b) turns out to be profile lines, then to determine their relative position, it is necessary to construct a third, profile projection of these lines. If we consider rice. 76, a, it is possible to mistakenly make the assumption that the lines AB and CD intersect. However, if we construct the profile projections of these straight lines, it will become clear that they intersect, since points 1 and 2 do not coincide, but are frontally competing points.

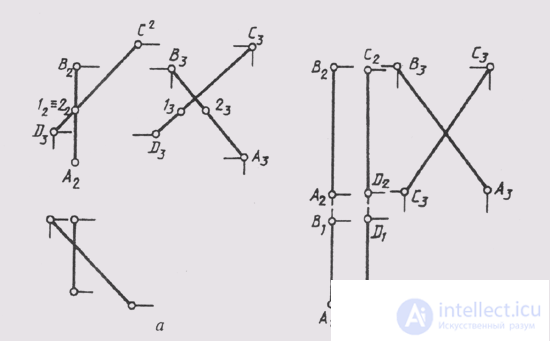
Fig. 76

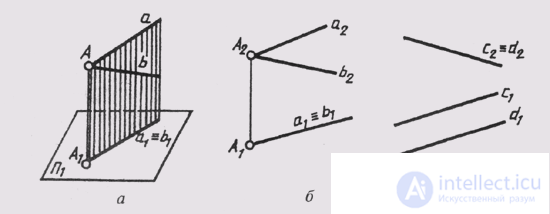
Fig. 77

Considering rice. 76, b it can be mistakenly assumed that the straight lines AB and CD are parallel. But after constructing their profile projections, we will see that they intersect, since on this plane their projections intersect.

Two straight lines, parallel or intersecting, can have a common projecting plane (Fig. 77, a). Then their images on the corresponding projection plane will coincide. Such straight lines are called competing:

a ^ b = A -> {a ₂ ^ b ₂ = A ₂ or a ₁ == b ₁ , A ₁ ~ a ₁ (b ₁ )}

The straight lines a and b horizontally competing have a common horizontal projecting plane (Fig. 77, b). The straight lines c and d (fig. 77, c) are frontally competing and have a common frontally projecting plane.