16. The division of the circle

In order to divide a circle into four equal parts, two mutually perpendicular diameters are drawn: at their intersection with the circle, we obtain points that divide the circle into four equal parts (Fig. 31, a).

To divide a circle into eight equal parts, arcs equal to the fourth part of the circle are divided in half. To do this, from two points bounding a quarter of the arc, as from the centers of the radii of a circle, perform serifs outside of its limits. The points obtained are connected to the center of the circles and at their intersection with the line of the circle they receive points dividing the quarter plots into half, i.e., they receive eight equal sections of the circle (Fig. 31 b).

The circle is divided into twelve equal parts as follows. Divide the circle into four parts mutually perpendicular diameters. Taking the point of intersection of diameters with a circle A, B, C, D for the centers, the radius of the four arcs to the intersection with the circle. The obtained points 1, 2, 3, 4, 5, 6, 7, 8 and points A, B, C, D divide the circle into twelve equal parts (Fig. 31, c).

Using the radius, it is easy to divide the circle into 3, 5, 6, 7 equal sections.

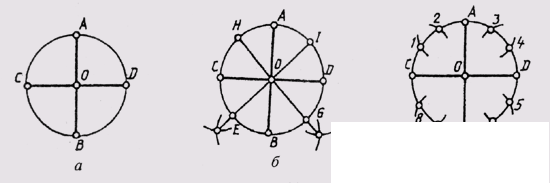
Fig. 31