74. Sweep prismatic and cylindrical surfaces

Sweep prismatic and cylindrical surfaces build method of normal section. The surface is dissected by a plane perpendicular to its generators (edges), and the true value of the normal section is determined. The line of the normal section is developed in a straight line. Then, when forming the surface (edges) of the surface, it is perpendicular to the scanning of the line of the normal section, which is taken as the base of reference for the sizes of the forming (edges).

In fig. 152 a full scan of the surfaces of the triangular prism ABCDEF is constructed . Since the side edges of the prisms BE, AD and CF are parallel to the plane P ₂ , they are shown in true length on the frontal plane of the projections. The plane of the normal section Sum (Sum ₂ ) is front projection. The normal section of the POR prism is built full-scale on the plane P ₄ , parallel to the plane Sum and perpendicular to the plane P ₂ . The line of the normal section is turned into a straight line and through the points P, Q, R, and P we draw straight lines perpendicular to the development of the line of the normal section. On each of the perpendiculars constructed, the segments of lateral edges measured on the plane P ₂ (to the normal section and after it) are laid on both sides of the line P P. Mark the points

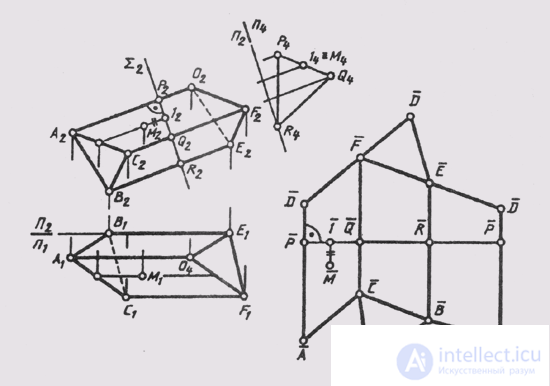
Fig. 152

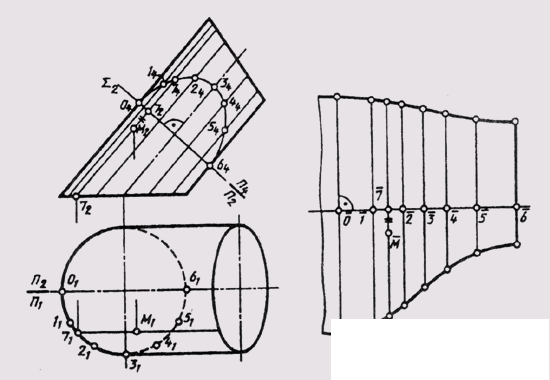
Fig. 153

edges on scan A and D; WITH and F; B and E, we connect them with straight line segments that give the true value of the sides of the base of the prism. Attaching both bases to the lateral surface of the prism (triangles A B C and DET ), we obtain a full scan of the prism. A point M belonging to the face of the ACFD prism is plotted on the prism scan with an auxiliary straight line parallel to the prism edges and intersecting the normal section at point 1.

In fig. 153 a sweep of the lateral surface of an elliptical cylinder, in which a twelve-sided prism is inscribed to construct a sweep, is constructed. The surface has a frontal plane of symmetry. The longest generator is zero, the shortest is the sixth, and the surface is cut through it. The sweep is a symmetrical figure with respect to the zero generator. The true value of half of the normal section of the surface of the Sum plane is built on the plane of the P ₄ - ellipse. We turn the arc of a semi-ellipse into a straight line 0 - 6 with the help of chords 0 ₄ - 1 ₄ , ... 5 ₄ - 6 ₄ , replacing the curved sections of the ellipse. At points 0 , 1 , ... 6 on the sweep, we restore the perpendicular

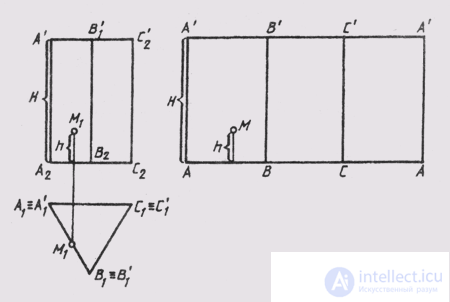
Fig. 154

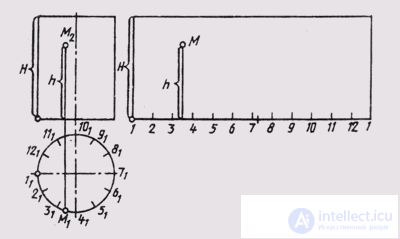
Fig. 155

Diculars, in which we lay the natural length of the sections forming the surface (up to the normal section and after it), measured on the plane P ₂ . The ends of the segments are joined by smooth curves that are a scan of the bases of the surface.

With the help of the seventh generatrix, a point of the surface is applied to the scan.

The construction of reamers of prismatic and cylindrical surfaces is greatly simplified if they are represented by simple straight figures. For an example in fig. 154 shows a scan of the triangular prizes of the correct form. We develop its sweeps using the fact that its AA, BB, SS ribs are parallel to the frontal plane of the projections and projected onto it in full size, and the lower ABC and upper A'B'C ' bases are parallel to the horizontal plane of the projections and projected onto it in full size . Point M on the development of a triangular prism is constructed in the usual way.

In fig. 155 is an example of the construction of a sweep of a right circular cylinder. Its height H on the frontal plane of the projections is projected in full size, and the lower and upper bases are parallel to the horizontal plane of the projections and projected on it in full size. In this case, we scan the cylindrical surface with the help of the chords connecting the adjacent division points of the base circle, into which a regular pentagon is inscribed. In this case, the cylindrical surface is conditionally replaced by the surface of an inscribed regular twelve-sided prism, and the scanning of the cylindrical surface is constructed by the method of triangulation.

The position of point M on the development of a cylindrical surface is determined in the usual way.