Symmetry relatively straight

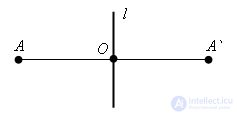
There is a straight line l and a point A not lying on a straight line. Drop from point A to line l perpendicular. On the continuation of this perpendicular, we postpone the segment OA` = OA. Point A` is symmetric to point A with respect to line l.



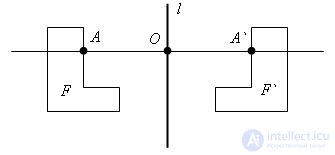
The transformation of symmetry with respect to the straight line l, is the transformation of the figure F into the figure F`, in which each of its points A goes to a point A` that is symmetrical with respect to the straight line l. Such figures F and F` are called symmetric with respect to the straight line l. If a transformation of a figure with respect to a straight line l translates it into itself, then this figure is called symmetric with respect to a given straight l, and the straight line l is called the axis of symmetry of the figure.



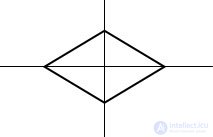
So the rhombus is symmetrical to itself with respect to its diagonals. Diagonal diamonds are its axes of symmetry.

See also

• Ball symmetry
• Central symmetry of the parallelepiped
• The symmetry property about a point
• Symmetry relatively straight
• Symmetry about point