Theorem If there are two non-zero collinear vectors, then there exists a number λ such that
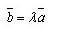 Evidence.
Evidence. Let a and b be equally directed.
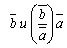
- These are vectors that are equally directed and have the same absolute value | b |. So they are equal:
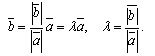
When vectors a and b are oppositely directed in the same way, we conclude that
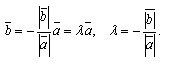
The theorem is proved.
Theorem Any vector with can be represented as
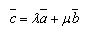
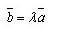
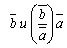
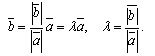
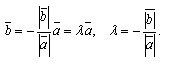
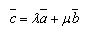
Comments
To leave a comment
Planometry
Terms: Planometry