Circumference described around a triangle

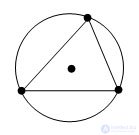
A circle is called a circumscribed triangle if it passes through all its vertices.



Theorem.

The center of the circle described around the triangle is the point of intersection of the perpendiculars to the sides of the triangle drawn through the midpoints of these sides.



Evidence.

Let ABC be a given triangle and O be the center of a circle described around a given triangle. Δ AOB - isosceles (AO = OB as radii). The median OD of this triangle is at the same time its height. Therefore, the center of the circle lies on a straight line, perpendicular to the side AC and passing through its middle. It is also proved that the center of the circle is perpendicular to the other sides of the triangle. The theorem is proved.