Convex polygons. Property

Theorem.

The sum of the angles of a convex n-gon is 180 ° * (n-2).



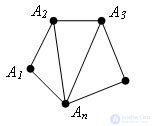Evidence.

It should be noted, n ≥ 3.
For n = 3 the polygon turns into a triangle and the theorem is valid.
For n> 3 we draw n-3 diagonals: A2An, A3An, ..., An-1An. We obtain n-2 triangles: Δ A1A2An, Δ A2A3An, ..., An-2An-1An. The sum of the angles of all triangles is equal to the sum of the angles of the polygon. Since the sum of the angles of the triangle is 180 ° and the number of triangles is n - 2, the sum of all the angles of the polygon is 180 ° * (n - 2). The theorem is proved.