Construction of a perpendicular straight line

Through point O, draw a straight line perpendicular to this straight line a.



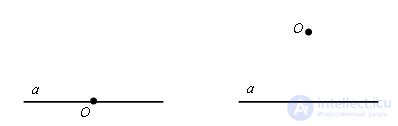
Two options are possible:
1. The point O lies on the line a;
2. The point O does not lie on the line a.

Decision.



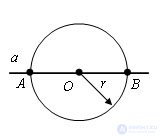
First option.
Draw a circle with an arbitrary radius r centered at the point O. The circle intersects the line at points A and B.



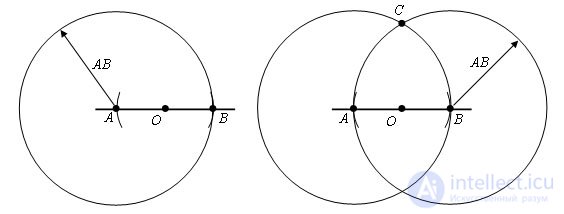
From points A and B we draw circles with radius AB. Let angst C - the intersection point of these circles.



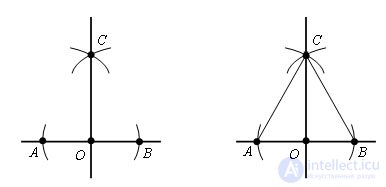
The required line passes through points C and O.
Evidence.
Draw AC and CB. Δ ACO = Δ BCO by the third sign of equality of triangles (AO = OB, AC = CB, by construction, CO is common). ∠ COA = ∠ COB = 90 °. Direct CO ⊥ AB.

The second option.



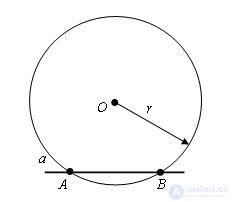
From point O we draw a circle with a certain radius r, so that the circle intersects the line a. Let A and B be the intersection points of the circle with the line a.



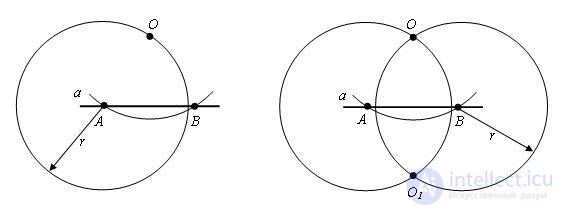
Let us draw circles with the same radius r with centers at points A and B. Let point O1 be the intersection point of these circles lying in the half-plane different from the one in which point O lies.



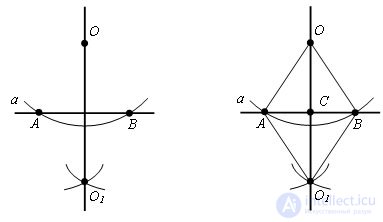
Draw through the points O and O1 a straight line. This will be the desired line. Evidence. Let the lines OO1 and AB intersect at point C. Δ AOB = Δ BO1A on the third sign of equality of triangles (AO = OB = AO1 = O1B, by construction, AB is common). It follows that ∠ OAС = ∠ O1AC. Δ OAC = Δ O1AC by the first sign of equality of triangles (AO = AO1, by construction, ∠ OAС = ∠ O1AC, AC - common). Therefore, ∠ OCA = ∠ O1CA, and since these angles are adjacent, they are straight. Therefore, OC is a perpendicular dropped from point O to the line a.