Theorem Homothety is a similarity transformation.
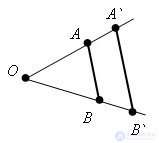 Evidence.
Evidence. Let O be the center of a homothety, k be the coefficient of a homothety, A and B be two arbitrary points of the figure.
With homothety, points A and B go to points A` and B` on the rays OA and OB, respectively, and OA` = k * OA, OB` = k * OB. Consequently
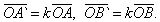
Then subtracting the equality term by term, we get:
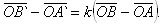
Because
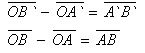
Thats
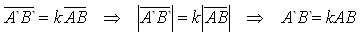
Therefore, homothety is a similarity transformation. The theorem is proved.

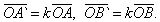
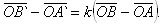
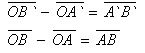
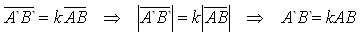
Comments
To leave a comment
Planometry
Terms: Planometry