Square. Sign of the square

A square is a rectangle in which all sides are equal.



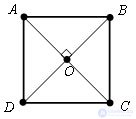
The square has the following properties:
1. the square has all the corners right;
2. the diagonals of the square are equal;
3. The diagonals of the square intersect at a right angle and are the bisectors of its angles.

AB = BC = CD = DA
∠ A = ∠ B = ∠ C = ∠ D = 90 °
AC ⊥ BD
AC = BD

Theorem.

If the diagonals of the rectangle intersect at a right angle, then this rectangle is a square.

Evidence.

The rectangle is a parallelogram, and a parallelogram whose diagonals intersect at right angles is a rhombus. Then the rhombus all sides are equal. So we have a rectangle in which all sides are equal, and by definition this is a square. The theorem is proved

See also

• Quadrilateral
• Parallelogram. Signs of parallelogram
• Rectangle area
• Trapezium
• Rectangle. Rectangle Tag
• Square. Sign of the square