Diamond property

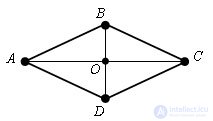
Theorem (properties of a rhombus).

Diagonal rhombus intersect at right angles. Diagonal rhombus are the bisectors of its angles.

Evidence.

Let ABCD be a given diamond. Diagonal diamonds intersect at point O.
By the property of the parallelogram AO = OC, then BO is the median Δ ABC. And since the triangle ABC is isosceles, by the properties of the median of an isosceles triangle conducted to the base, BO is also a height and a bisector. Hence the straight line BO ⊥ AC and ∠ ABO = CBO. The theorem is proved.

See also

• Diamond property
• Rectangle properties
• Parallelogram properties
• Rectangle. Rectangle Tag
• Parallelogram. Signs of parallelogram